| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 2 Relations And Functions
This dedicated solutions page offers indispensable and detailed guidance for mastering Chapter 2: Relations and Functions, a pivotal area of study within the Class 11 curriculum as outlined in the Latest NCERT (2024-25) mathematics textbook. Understanding the intricate concepts of relations and, more specifically, functions is absolutely crucial for building a strong foundation for calculus and advanced mathematical topics. These solutions are meticulously prepared to demystify these concepts, providing clarity and step-by-step assistance for every exercise, fully aligning with the rationalized syllabus effective from the 2023-24 session onwards and continued in the current edition. All topics presented herein are part of the official updated curriculum.
The exploration commences with the fundamental concept of the Cartesian Product of sets. We clarify how to determine $A \times B = \{(a, b) \mid a \in A \text{ and } b \in B\}$, the set of all possible ordered pairs formed by taking the first element from set $A$ and the second element from set $B$. The solutions provide clear demonstrations and examples, ensuring you grasp how this product forms the bedrock upon which relations are defined. Building directly on this, a Relation $R$ from a non-empty set $A$ to a non-empty set $B$ is formally introduced and explained as any subset of the Cartesian product $A \times B$, that is, $R \subseteq A \times B$. You will find comprehensive guidance on representing these relations accurately using both the Roster Form (listing the specific ordered pairs belonging to the relation) and the Set-builder Form (describing the rule or property connecting the elements of the ordered pairs).
A critical skill emphasized throughout these solutions is the determination of the Domain and Range of a given relation. The domain is clearly defined as the set of all first components (or pre-images) present in the ordered pairs of $R$, while the range is the set of all second components (or images). The solutions walk you through the process of identifying these sets from the relation's definition or representation. Subsequently, the transition from the general concept of relations to the more specialized and highly significant concept of Functions is carefully articulated. The defining characteristic of a function – that every element in the domain must correspond to exactly one unique element in the codomain – is stressed. Solutions provide practical methods and checks to help students rigorously identify whether a given relation qualifies as a function, a distinction vital for further study.
A significant portion of this resource is dedicated to exploring various essential types of real-valued functions, providing a deep dive into their properties as covered in the Latest NCERT (2024-25):
- The Identity Function: $f(x) = x$.
- The Constant Function: $f(x) = c$, where $c$ is a constant.
- Polynomial Functions: Functions defined by polynomials, like $f(x) = a_n x^n + \dots + a_1 x + a_0$.
- Rational Functions: Functions expressed as a ratio of two polynomials, $f(x) = \frac{P(x)}{Q(x)}$, with the condition $Q(x) \neq 0$.
- The Modulus Function: $f(x) = |x|$.
- The Signum Function.
- The Greatest Integer Function: $f(x) = [x]$ (or $\lfloor x \rfloor$).
Detailed methodologies are presented for finding the specific domain (permissible input values) and range (resulting output values) for these standard functions, as well as for other functions defined algebraically. Where relevant, the graphical representations of these standard functions are often discussed or illustrated, fostering a visual intuition for their behavior and characteristics.
Furthermore, the solutions thoroughly cover the Algebra of Real Functions, a topic retained in the rationalized syllabus. Step-by-step procedures demonstrate how to perform arithmetic operations on two real functions, $f$ and $g$:
- Addition: $(f+g)(x) = f(x) + g(x)$
- Subtraction: $(f-g)(x) = f(x) - g(x)$
- Multiplication: $(fg)(x) = f(x) \cdot g(x)$
- Division (Quotient): $(\frac{f}{g})(x) = \frac{f(x)}{g(x)}$
Example 1 to 6 (Before Exercise 2.1)
Example 1: If (x + 1, y – 2) = (3,1), find the values of x and y.
Answer:
Given:
The given equation is $(x + 1, y – 2) = (3,1)$.
To Find:
The values of $x$ and $y$.
Solution:
When two ordered pairs are equal, their corresponding elements are equal.
Therefore, we equate the first elements and the second elements separately.
$x + 1 = 3$
(Equating the first elements)
Subtract 1 from both sides of the equation:
$x = 3 - 1$
$x = 2$
... (i)
$\mathrm{y} – 2 = 1$
(Equating the second elements)
Add 2 to both sides of the equation:
$\mathrm{y} = 1 + 2$
$\mathrm{y} = 3$
... (ii)
Thus, the values are $\mathrm{x} = 2$ and $\mathrm{y} = 3$.
Example 2: If P = {a, b, c} and Q = {r}, form the sets P × Q and Q × P. Are these two products equal?
Answer:
Given:
Set P = $\{a, b, c\}$
Set Q = $\{r\}$
To Find:
The sets P $\times$ Q and Q $\times$ P.
Whether P $\times$ Q = Q $\times$ P.
Solution:
The Cartesian product of two non-empty sets A and B is the set of all ordered pairs $(x, y)$ such that $x \in A$ and $y \in B$. It is denoted by A $\times$ B.
P $\times$ Q is the set of ordered pairs $(p, q)$ where $p \in P$ and $q \in Q$.
P $\times$ Q = $\{a, b, c\} \times \{r\}$
P $\times$ Q = $\{(a, r), (b, r), (c, r)\}$.
Q $\times$ P is the set of ordered pairs $(q, p)$ where $q \in Q$ and $p \in P$.
Q $\times$ P = $\{r\} \times \{a, b, c\}$
Q $\times$ P = $\{(r, a), (r, b), (r, c)\}$.
Now we compare the elements of P $\times$ Q and Q $\times$ P.
The elements of P $\times$ Q are $(a, r), (b, r), (c, r)$.
The elements of Q $\times$ P are $(r, a), (r, b), (r, c)$.
For two ordered pairs to be equal, their corresponding components must be equal. For example, $(a, r)$ is not equal to $(r, a)$ unless $a = r$, which is not the case here.
Since the ordered pairs in P $\times$ Q are different from the ordered pairs in Q $\times$ P, the two sets are not equal.
Therefore, P $\times$ Q $\neq$ Q $\times$ P.
Example 3: Let A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}. Find
(i) A × (B ∩ C)
(ii) (A × B) ∩ (A × C)
(iii) A × (B ∪ C)
(iv) (A × B) ∪ (A × C)
Answer:
Given:
Set A = $\{1, 2, 3\}$
Set B = $\{3, 4\}$
Set C = $\{4, 5, 6\}$
To Find:
(i) A $\times$ (B $\cap$ C)
(ii) (A $\times$ B) $\cap$ (A $\times$ C)
(iii) A $\times$ (B $\cup$ C)
(iv) (A $\times$ B) $\cup$ (A $\times$ C)
Solution:
First, we determine the sets resulting from the operations on B and C.
The intersection of B and C is the set of elements common to both B and C.
$B \cap C = \{3, 4\} \cap \{4, 5, 6\}$
$B \cap C = \{4\}$.
The union of B and C is the set containing all elements from B or C (or both).
$B \cup C = \{3, 4\} \cup \{4, 5, 6\}$
$B \cup C = \{3, 4, 5, 6\}$.
Next, we find the Cartesian products A $\times$ B and A $\times$ C.
A $\times$ B is the set of all ordered pairs $(a, b)$ where $a \in A$ and $b \in B$.
$A \times B = \{1, 2, 3\} \times \{3, 4\}$
$A \times B = \{(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)\}$.
A $\times$ C is the set of all ordered pairs $(a, c)$ where $a \in A$ and $c \in C$.
$A \times C = \{1, 2, 3\} \times \{4, 5, 6\}$
$A \times C = \{(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)\}$.
Now we can compute the required expressions.
(i) A × (B ∩ C)
We use set A and the calculated set B $\cap$ C.
$A \times (B \cap C) = \{1, 2, 3\} \times \{4\}$
$A \times (B \cap C) = \{(1, 4), (2, 4), (3, 4)\}$.
(ii) (A × B) ∩ (A × C)
We find the intersection of the sets A $\times$ B and A $\times$ C that we calculated.
$(A \times B) \cap (A \times C) = \{(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)\} \cap \{(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)\}$
The common elements are the ordered pairs that appear in both sets.
$(A \times B) \cap (A \times C) = \{(1, 4), (2, 4), (3, 4)\}$.
Note that $A \times (B \cap C) = (A \times B) \cap (A \times C)$, illustrating a property of Cartesian products and set intersection.
(iii) A × (B ∪ C)
We use set A and the calculated set B $\cup$ C.
$A \times (B \cup C) = \{1, 2, 3\} \times \{3, 4, 5, 6\}$
$A \times (B \cup C) = \{(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)\}$.
(iv) (A × B) ∪ (A × C)
We find the union of the sets A $\times$ B and A $\times$ C that we calculated.
$(A \times B) \cup (A \times C) = \{(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)\} \cup \{(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)\}$
The union contains all unique elements from both sets.
$(A \times B) \cup (A \times C) = \{(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)\}$.
Note that $A \times (B \cup C) = (A \times B) \cup (A \times C)$, illustrating another property of Cartesian products and set union.
Example 4: If P = {1, 2}, form the set P × P × P
Answer:
Given:
Set P = $\{1, 2\}$
To Find:
The set P $\times$ P $\times$ P.
Solution:
The Cartesian product of three sets A, B, and C, denoted by A $\times$ B $\times$ C, is the set of all ordered triples $(a, b, c)$ where $a \in A$, $b \in B$, and $c \in C$.
In this case, we are finding P $\times$ P $\times$ P, which is the set of all ordered triples $(p_1, p_2, p_3)$ where $p_1 \in P$, $p_2 \in P$, and $p_3 \in P$.
P $\times$ P $\times$ P = $\{1, 2\} \times \{1, 2\} \times \{1, 2\}$.
To find the elements of P $\times$ P $\times$ P, we list all possible ordered triples where each component is either 1 or 2.
We can think of this by first finding P $\times$ P:
$P \times P = \{(1, 1), (1, 2), (2, 1), (2, 2)\}$
Now, we find (P $\times$ P) $\times$ P, forming triples with elements from P $\times$ P and P:
$(P \times P) \times P = \{(1, 1), (1, 2), (2, 1), (2, 2)\} \times \{1, 2\}$
For each element in P $\times$ P, we combine it with each element in P to form a triple:
- From $(1, 1)$ and 1: $(1, 1, 1)$
- From $(1, 1)$ and 2: $(1, 1, 2)$
- From $(1, 2)$ and 1: $(1, 2, 1)$
- From $(1, 2)$ and 2: $(1, 2, 2)$
- From $(2, 1)$ and 1: $(2, 1, 1)$
- From $(2, 1)$ and 2: $(2, 1, 2)$
- From $(2, 2)$ and 1: $(2, 2, 1)$
- From $(2, 2)$ and 2: $(2, 2, 2)$
Thus, the set P $\times$ P $\times$ P is:
P $\times$ P $\times$ P = $\{(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)\}$.
The number of elements in P $\times$ P $\times$ P is $|P| \times |P| \times |P| = 2 \times 2 \times 2 = 8$, which matches the number of ordered triples listed.
Example 5: If R is the set of all real numbers, what do the cartesian products R × R and R × R × R represent?
Answer:
Given:
R is the set of all real numbers.
To Represent:
The representation of the Cartesian products R $\times$ R and R $\times$ R $\times$ R.
Representation:
The Cartesian product of two sets A and B, denoted by A $\times$ B, is the set of all ordered pairs $(a, b)$ where $a \in A$ and $b \in B$.
For R $\times$ R:
R $\times$ R = $\{(x, y) \mid x \in R \text{ and } y \in R\}$.
This set consists of all possible ordered pairs of real numbers.
Geometrically, each ordered pair $(x, y)$ of real numbers corresponds to a unique point in a two-dimensional coordinate system, commonly known as the Cartesian plane.
Therefore, R $\times$ R represents the entire two-dimensional Cartesian plane.
For R $\times$ R $\times$ R:
R $\times$ R $\times$ R = $\{(x, y, z) \mid x \in R, y \in R, \text{ and } z \in R\}$.
This set consists of all possible ordered triples of real numbers.
Geometrically, each ordered triple $(x, y, z)$ of real numbers corresponds to a unique point in a three-dimensional coordinate system.
Therefore, R $\times$ R $\times$ R represents the entire three-dimensional space.
Example 6: If A × B ={(p, q), (p, r), (m, q), (m, r)}, find A and B.
Answer:
Given:
The Cartesian product A $\times$ B = $\{(p, q), (p, r), (m, q), (m, r)\}$.
To Find:
The sets A and B.
Solution:
The Cartesian product A $\times$ B is defined as the set of all ordered pairs $(a, b)$ where $a \in A$ and $b \in B$.
From the given set A $\times$ B, the first element of each ordered pair belongs to set A, and the second element of each ordered pair belongs to set B.
To find set A, we collect all the first elements of the ordered pairs in A $\times$ B:
First elements are p, p, m, m.
(from the ordered pairs)
The set A consists of the unique elements from this collection.
A = $\{p, m\}$.
To find set B, we collect all the second elements of the ordered pairs in A $\times$ B:
Second elements are q, r, q, r.
(from the ordered pairs)
The set B consists of the unique elements from this collection.
B = $\{q, r\}$.
Thus, the sets are A = {p, m} and B = {q, r}.
We can verify this by forming A $\times$ B from the sets A and B we found:
A $\times$ B = $\{p, m\} \times \{q, r\} = \{(p, q), (p, r), (m, q), (m, r)\}$.
This matches the given A $\times$ B, confirming our result.
Exercise 2.1
Question 1. If $\left( \frac{x}{3}+1 , \;y \;-\; \frac{2}{3} \right) = \left( \frac{5}{3},\frac{1}{3} \right)$ , find the values of x and y.
Answer:
Given:
The given equation is $\left( \frac{x}{3}+1 , \;y \;-\; \frac{2}{3} \right) = \left( \frac{5}{3},\frac{1}{3} \right)$.
To Find:
The values of $x$ and $y$.
Solution:
When two ordered pairs are equal, their corresponding elements are equal.
Equating the first components:
$\frac{x}{3} + 1 = \frac{5}{3}$
... (i)
From equation (i), subtract 1 from both sides:
$\frac{x}{3} = \frac{5}{3} - 1$
$\frac{x}{3} = \frac{5}{3} - \frac{3}{3}$
$\frac{x}{3} = \frac{5 - 3}{3}$
$\frac{x}{3} = \frac{2}{3}$
Multiply both sides by 3:
$x = \frac{2}{3} \times 3$
$x = 2$
Equating the second components:
$\mathrm{y} - \frac{2}{3} = \frac{1}{3}$
... (ii)
From equation (ii), add $\frac{2}{3}$ to both sides:
$\mathrm{y} = \frac{1}{3} + \frac{2}{3}$
$\mathrm{y} = \frac{1 + 2}{3}$
$\mathrm{y} = \frac{3}{3}$
$\mathrm{y} = 1$
Thus, the values are $x = 2$ and $y = 1$.
Question 2. If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A × B).
Answer:
Given:
The number of elements in set A is 3.
Set B = $\{3, 4, 5\}$.
To Find:
The number of elements in (A $\times$ B).
Solution:
Let $|A|$ denote the number of elements in set A.
We are given that $|A| = 3$.
Let $|B|$ denote the number of elements in set B.
The set B is given as $\{3, 4, 5\}$. By counting the distinct elements, we find that $|B| = 3$.
The number of elements in the Cartesian product of two sets A and B is given by the product of the number of elements in A and the number of elements in B.
Mathematically, the formula is: $|A \times B| = |A| \times |B|$.
Substitute the values of $|A|$ and $|B|$ into the formula:
$|A \times B| = 3 \times 3$
$|A \times B| = 9$
Therefore, the number of elements in (A $\times$ B) is 9.
Question 3. If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
Answer:
Given:
Set G = $\{7, 8\}$
Set H = $\{5, 4, 2\}$
To Find:
The sets G $\times$ H and H $\times$ G.
Solution:
The Cartesian product of two non-empty sets A and B, denoted by A $\times$ B, is the set of all ordered pairs $(a, b)$ such that $a \in A$ and $b \in B$.
To find G $\times$ H, we form all possible ordered pairs with the first element from G and the second element from H.
$G \times H = \{7, 8\} \times \{5, 4, 2\}$
$G \times H = \{(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)\}$.
To find H $\times$ G, we form all possible ordered pairs with the first element from H and the second element from G.
$H \times G = \{5, 4, 2\} \times \{7, 8\}$
$H \times G = \{(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)\}$.
Thus, the sets are:
G $\times$ H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
H $\times$ G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}
Question 4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ φ) = φ.
Answer:
(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.
Given:
Set P = $\{m, n\}$
Set Q = $\{n, m\}$
Evaluation:
The set Q = $\{n, m\}$ is the same as the set Q = $\{m, n\}$. Thus, P = $\{m, n\}$ and Q = $\{m, n\}$.
The Cartesian product P $\times$ Q is the set of all ordered pairs $(p, q)$ where $p \in P$ and $q \in Q$.
P $\times$ Q = $\{m, n\} \times \{m, n\}$
P $\times$ Q = $\{(m, m), (m, n), (n, m), (n, n)\}$.
The given statement says P $\times$ Q = $\{(m, n), (n, m)\}$. This is not the complete set of ordered pairs.
Therefore, the statement is False.
Correct Statement:
If P = {m, n} and Q = { n, m}, then P $\times$ Q = {(m, m), (m, n), (n, m), (n, n)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
Given:
A and B are non-empty sets.
Evaluation:
By the definition of the Cartesian product, A $\times$ B is the set of all ordered pairs $(x, y)$ where $x \in A$ and $y \in B$.
If A is non-empty, there exists at least one element $a \in A$.
If B is non-empty, there exists at least one element $b \in B$.
Since there is at least one element in A and at least one element in B, we can form at least one ordered pair $(a, b)$ where $a \in A$ and $b \in B$. This ordered pair $(a, b)$ is an element of A $\times$ B.
Since A $\times$ B contains at least one element, it is a non-empty set.
The statement accurately describes the Cartesian product of non-empty sets.
Therefore, the statement is True.
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ φ) = φ.
Given:
Set A = $\{1, 2\}$
Set B = $\{3, 4\}$
Evaluation:
First, we find the intersection of set B and the empty set $\phi$.
The intersection of any set with the empty set is always the empty set.
$B \cap \phi = \{3, 4\} \cap \phi = \phi$.
Now, we find the Cartesian product of set A and the resulting set from the intersection, which is $\phi$.
A $\times$ (B $\cap$ $\phi$) = A $\times$ $\phi$.
The Cartesian product of any non-empty set with the empty set is always the empty set, because there are no elements in the empty set to form ordered pairs with the elements from the non-empty set.
A $\times$ $\phi = \{1, 2\} \times \phi = \phi$.
The given statement says A $\times$ (B $\cap$ $\phi$) = $\phi$. This matches our calculation.
Therefore, the statement is True.
Question 5. If A = {–1, 1}, find A × A × A.
Answer:
Given:
Set A = $\{-1, 1\}$.
To Find:
The set A $\times$ A $\times$ A.
Solution:
The Cartesian product A $\times$ A $\times$ A is the set of all ordered triples $(a_1, a_2, a_3)$ where $a_1 \in A$, $a_2 \in A$, and $a_3 \in A$.
Since A = $\{-1, 1\}$, each component of the ordered triple can be either -1 or 1.
We can list all possible combinations:
- When the first element is -1:
- (-1, -1, -1)
- (-1, -1, 1)
- (-1, 1, -1)
- (-1, 1, 1)
- When the first element is 1:
- (1, -1, -1)
- (1, -1, 1)
- (1, 1, -1)
- (1, 1, 1)
Alternatively, we can find A $\times$ A first:
$A \times A = \{-1, 1\} \times \{-1, 1\} = \{(-1, -1), (-1, 1), (1, -1), (1, 1)\}$.
Then, A $\times$ A $\times$ A is (A $\times$ A) $\times$ A:
$(A \times A) \times A = \{(-1, -1), (-1, 1), (1, -1), (1, 1)\} \times \{-1, 1\}$.
Forming triples:
- $(-1, -1)$ with $-1 \implies (-1, -1, -1)$
- $(-1, -1)$ with $1 \implies (-1, -1, 1)$
- $(-1, 1)$ with $-1 \implies (-1, 1, -1)$
- $(-1, 1)$ with $1 \implies (-1, 1, 1)$
- $(1, -1)$ with $-1 \implies (1, -1, -1)$
- $(1, -1)$ with $1 \implies (1, -1, 1)$
- $(1, 1)$ with $-1 \implies (1, 1, -1)$
- $(1, 1)$ with $1 \implies (1, 1, 1)$
Thus, the set A $\times$ A $\times$ A is:
$A \times A \times A = \{ (-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1) \}$.
The number of elements in A is $|A| = 2$. The number of elements in A $\times$ A $\times$ A is $|A|^3 = 2^3 = 8$, which matches the number of ordered triples we found.
Question 6. If A × B = {(a, x),(a , y), (b, x), (b, y)}. Find A and B.
Answer:
Given:
The Cartesian product A $\times$ B = $\{(a, x), (a , y), (b, x), (b, y)\}$.
To Find:
The sets A and B.
Solution:
The Cartesian product of two sets A and B, denoted by A $\times$ B, is defined as the set of all ordered pairs $(m, n)$ where $m \in A$ and $n \in B$.
From the definition, the set A consists of all the first components of the ordered pairs in A $\times$ B.
The first components in the given set A $\times$ B are $a, a, b, b$.
To form set A, we list the unique first components.
A = $\{a, b\}$
(Collection of unique first elements)
The set B consists of all the second components of the ordered pairs in A $\times$ B.
The second components in the given set A $\times$ B are $x, y, x, y$.
To form set B, we list the unique second components.
B = $\{x, y\}$
(Collection of unique second elements)
Thus, the sets are A = {a, b} and B = {x, y}.
We can verify our answer by computing A $\times$ B using the sets we found:
$A \times B = \{a, b\} \times \{x, y\} = \{(a, x), (a, y), (b, x), (b, y)\}$.
This matches the given A $\times$ B, confirming our solution.
Question 7. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that
(i) A × (B ∩ C) = (A × B) ∩ (A × C).
(ii) A × C is a subset of B × D.
Answer:
Given:
Set A = $\{1, 2\}$
Set B = $\{1, 2, 3, 4\}$
Set C = $\{5, 6\}$
Set D = $\{5, 6, 7, 8\}$
To Verify:
(i) A $\times$ (B $\cap$ C) = (A $\times$ B) $\cap$ (A $\times$ C)
(ii) A $\times$ C $\subseteq$ B $\times$ D
Solution:
Part (i): Verify A × (B ∩ C) = (A × B) ∩ (A × C)
First, let's find B $\cap$ C:
$B \cap C = \{1, 2, 3, 4\} \cap \{5, 6\}$
The intersection of sets B and C contains elements that are in both sets. There are no common elements.
$B \cap C = \phi$
Now, let's find A $\times$ (B $\cap$ C):
$A \times (B \cap C) = A \times \phi$
The Cartesian product of any set with the empty set is the empty set.
$A \times (B \cap C) = \phi$
Next, let's find A $\times$ B:
$A \times B = \{1, 2\} \times \{1, 2, 3, 4\}$
$A \times B = \{(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)\}$
Now, let's find A $\times$ C:
$A \times C = \{1, 2\} \times \{5, 6\}$
$A \times C = \{(1, 5), (1, 6), (2, 5), (2, 6)\}$
Finally, let's find the intersection of A $\times$ B and A $\times$ C:
$(A \times B) \cap (A \times C) = \{(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)\} \cap \{(1, 5), (1, 6), (2, 5), (2, 6)\}$
The intersection contains the ordered pairs that are common to both sets. Comparing the elements, we find there are no common ordered pairs.
$(A \times B) \cap (A \times C) = \phi$
Comparing the results:
A $\times$ (B $\cap$ C) = $\phi$
(A $\times$ B) $\cap$ (A $\times$ C) = $\phi$
Since both results are the empty set, they are equal.
Thus, the statement A × (B ∩ C) = (A × B) ∩ (A × C) is verified.
Part (ii): Verify A × C is a subset of B × D
For A $\times$ C to be a subset of B $\times$ D (A $\times$ C $\subseteq$ B $\times$ D), every element of A $\times$ C must also be an element of B $\times$ D.
An element $(x, y)$ is in A $\times$ C if $x \in A$ and $y \in C$.
An element $(x, y)$ is in B $\times$ D if $x \in B$ and $y \in D$.
From Part (i), we found A $\times$ C:
$A \times C = \{(1, 5), (1, 6), (2, 5), (2, 6)\}$
Now, let's find B $\times$ D:
$B \times D = \{1, 2, 3, 4\} \times \{5, 6, 7, 8\}$
$B \times D = \{(1, 5), (1, 6), (1, 7), (1, 8),$
$(2, 5), (2, 6), (2, 7), (2, 8),$
$(3, 5), (3, 6), (3, 7), (3, 8),$
$(4, 5), (4, 6), (4, 7), (4, 8)\}$
Now we check if every element in A $\times$ C is present in B $\times$ D.
- $(1, 5) \in A \times C$. Is $(1, 5) \in B \times D$? Yes, because $1 \in B$ and $5 \in D$.
- $(1, 6) \in A \times C$. Is $(1, 6) \in B \times D$? Yes, because $1 \in B$ and $6 \in D$.
- $(2, 5) \in A \times C$. Is $(2, 5) \in B \times D$? Yes, because $2 \in B$ and $5 \in D$.
- $(2, 6) \in A \times C$. Is $(2, 6) \in B \times D$? Yes, because $2 \in B$ and $6 \in D$.
Since every ordered pair in A $\times$ C is also present in B $\times$ D, A $\times$ C is a subset of B $\times$ D.
This is because $A \subseteq B$ (since $\{1, 2\} \subseteq \{1, 2, 3, 4\}$) and $C \subseteq D$ (since $\{5, 6\} \subseteq \{5, 6, 7, 8\}$). If $A \subseteq B$ and $C \subseteq D$, then $A \times C \subseteq B \times D$.
Thus, the statement A × C is a subset of B × D is verified.
Question 8. Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.
Answer:
Given:
Set A = $\{1, 2\}$
Set B = $\{3, 4\}$
To Find:
A $\times$ B.
The number of subsets of A $\times$ B.
List all subsets of A $\times$ B.
Solution:
First, we find the Cartesian product A $\times$ B. It is the set of all ordered pairs $(a, b)$ where $a \in A$ and $b \in B$.
$A \times B = \{1, 2\} \times \{3, 4\}$
$A \times B = \{(1, 3), (1, 4), (2, 3), (2, 4)\}$.
Next, we find the number of elements in A $\times$ B. Let $n(|A \times B|)$ be the number of elements.
$|A| = 2$ (number of elements in A)
$|B| = 2$ (number of elements in B)
$|A \times B| = |A| \times |B| = 2 \times 2 = 4$.
The set A $\times$ B has 4 elements: $(1, 3), (1, 4), (2, 3), (2, 4)$.
The number of subsets of a set with $m$ elements is $2^m$.
Since $|A \times B| = 4$, the number of subsets of A $\times$ B is $2^4$.
$2^4 = 2 \times 2 \times 2 \times 2 = 16$.
The set A $\times$ B will have 16 subsets.
Finally, we list all the subsets of A $\times$ B. Let the elements of A $\times$ B be $e_1=(1, 3), e_2=(1, 4), e_3=(2, 3), e_4=(2, 4)$.
Subsets with 0 elements (the empty set):
$\phi$
Subsets with 1 element:
$\{(1, 3)\}$, $\{(1, 4)\}$, $\{(2, 3)\}$, $\{(2, 4)\}$
Subsets with 2 elements:
$\{(1, 3), (1, 4)\}$, $\{(1, 3), (2, 3)\}$, $\{(1, 3), (2, 4)\}$,
$\{(1, 4), (2, 3)\}$, $\{(1, 4), (2, 4)\}$, $\{(2, 3), (2, 4)\}$
Subsets with 3 elements:
$\{(1, 3), (1, 4), (2, 3)\}$, $\{(1, 3), (1, 4), (2, 4)\}$,
$\{(1, 3), (2, 3), (2, 4)\}$, $\{(1, 4), (2, 3), (2, 4)\}$
Subsets with 4 elements (the set itself):
$\{(1, 3), (1, 4), (2, 3), (2, 4)\}$
Listing all 16 subsets:
Subsets of A $\times$ B:
$\phi$, $\{(1, 3)\}$, $\{(1, 4)\}$, $\{(2, 3)\}$, $\{(2, 4)\}$,
$\{(1, 3), (1, 4)\}$, $\{(1, 3), (2, 3)\}$, $\{(1, 3), (2, 4)\}$, $\{(1, 4), (2, 3)\}$, $\{(1, 4), (2, 4)\}$, $\{(2, 3), (2, 4)\}$,
$\{(1, 3), (1, 4), (2, 3)\}$, $\{(1, 3), (1, 4), (2, 4)\}$, $\{(1, 3), (2, 3), (2, 4)\}$, $\{(1, 4), (2, 3), (2, 4)\}$,
$\{(1, 3), (1, 4), (2, 3), (2, 4)\}$.
Question 9. Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
Answer:
Given:
$n(A) = 3$
$n(B) = 2$
The ordered pairs $(x, 1), (y, 2), (z, 1)$ are elements of A $\times$ B.
$x, y,$ and $z$ are distinct elements.
To Find:
Set A and Set B.
Solution:
The Cartesian product A $\times$ B is defined as the set of all ordered pairs $(a, b)$ where $a \in A$ and $b \in B$.
The first component of each ordered pair in A $\times$ B belongs to the set A.
The given ordered pairs that are in A $\times$ B are $(x, 1), (y, 2),$ and $(z, 1)$.
The first components of these ordered pairs are $x, y,$ and $z$.
Since $(x, 1) \in A \times B$, it implies that $x \in A$.
Since $(y, 2) \in A \times B$, it implies that $y \in A$.
Since $(z, 1) \in A \times B$, it implies that $z \in A$.
We are given that $x, y,$ and $z$ are distinct elements, and that the set A has exactly 3 elements, i.e., $n(A) = 3$.
Since $x, y,$ and $z$ are three distinct elements that belong to set A, and A contains exactly 3 elements, set A must be comprised of precisely these elements.
Therefore, A = {x, y, z}.
The second component of each ordered pair in A $\times$ B belongs to the set B.
The second components of the given ordered pairs $(x, 1), (y, 2),$ and $(z, 1)$ are $1, 2,$ and $1$.
The unique second components observed from these ordered pairs are $1$ and $2$.
Since $(x, 1) \in A \times B$, it implies that $1 \in B$.
Since $(y, 2) \in A \times B$, it implies that $2 \in B$.
Since $(z, 1) \in A \times B$, it implies that $1 \in B$, which is consistent with $1 \in B$.
We are given that set B has exactly 2 elements, i.e., $n(B) = 2$.
Since $1$ and $2$ are two distinct elements that belong to set B, and B contains exactly 2 elements, set B must be comprised of precisely these elements.
Therefore, B = {1, 2}.
To verify, the Cartesian product of A = $\{x, y, z\}$ and B = $\{1, 2\}$ is:
$A \times B = \{x, y, z\} \times \{1, 2\} = \{(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)\}$.
The given elements $(x, 1), (y, 2),$ and $(z, 1)$ are indeed present in the calculated set A $\times$ B.
The number of elements in A $\times$ B is $|A| \times |B| = 3 \times 2 = 6$, which matches the size of the calculated set A $\times$ B.
The sets are A = {x, y, z} and B = {1, 2}.
Question 10. The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.
Answer:
Given:
The Cartesian product A $\times$ A has 9 elements, i.e., $|A \times A| = 9$.
The ordered pairs $(-1, 0)$ and $(0, 1)$ are elements of A $\times$ A.
To Find:
The set A.
The remaining elements of A $\times$ A.
Solution:
The number of elements in the Cartesian product of a set A with itself is given by the square of the number of elements in set A.
$|A \times A| = |A| \times |A| = |A|^2$
We are given that $|A \times A| = 9$.
$|A|^2 = 9$
Taking the square root of both sides:
$|A| = \sqrt{9}$
$|A| = 3$
So, set A has 3 elements.
The Cartesian product A $\times$ A is the set of all ordered pairs $(a_1, a_2)$ where $a_1 \in A$ and $a_2 \in A$.
We are given that $(-1, 0) \in A \times A$. This implies that the first component, $-1$, must be in A, and the second component, $0$, must be in A.
$-1 \in A$
(From the first element of $(-1, 0)$)
$0 \in A$
(From the second element of $(-1, 0)$)
We are also given that $(0, 1) \in A \times A$. This implies that the first component, $0$, must be in A, and the second component, $1$, must be in A.
$0 \in A$
(From the first element of $(0, 1)$)
$1 \in A$
(From the second element of $(0, 1)$)
From the given elements, we know that $-1, 0,$ and $1$ must be in set A. These are three distinct elements.
Since we determined that set A has exactly 3 elements ($|A|=3$), and we have identified three distinct elements that must be in A, the set A must be exactly these three elements.
Therefore, A = {-1, 0, 1}.
Now we find the complete Cartesian product A $\times$ A using the set A = $\{-1, 0, 1\}$.
$A \times A = \{-1, 0, 1\} \times \{-1, 0, 1\}$
$A \times A = \{(-1, -1), (-1, 0), (-1, 1),$
$(0, -1), (0, 0), (0, 1),$
$(1, -1), (1, 0), (1, 1)\}$.
This set contains $3 \times 3 = 9$ elements, as expected.
The given elements are $(-1, 0)$ and $(0, 1)$.
The remaining elements in A $\times$ A are all elements except $(-1, 0)$ and $(0, 1)$.
The remaining elements are:
(-1, -1), (-1, 1), (0, -1), (0, 0), (1, -1), (1, 0), (1, 1).
Example 7 to 9 (Before Exercise 2.2)
Example 7: Let A = {1, 2, 3, 4, 5, 6}. Define a relation R from A to A by R = {(x, y) : y = x + 1 }
(i) Depict this relation using an arrow diagram.
(ii) Write down the domain, codomain and range of R.
Answer:
Given:
Set A = $\{1, 2, 3, 4, 5, 6\}$.
Relation R from A to A defined by R = $\{(x, y) : y = x + 1 \text{ and } x, y \in A\}$.
To Find:
(i) Arrow diagram representation of R.
(ii) Domain, codomain, and range of R.
Solution:
The relation R is defined by the rule $y = x + 1$, where both $x$ and $y$ must be elements of set A = $\{1, 2, 3, 4, 5, 6\}$.
We list the ordered pairs $(x, y)$ that satisfy this condition:
- If $x = 1$, $y = 1 + 1 = 2$. Since $1 \in A$ and $2 \in A$, the ordered pair $(1, 2)$ is in R.
- If $x = 2$, $y = 2 + 1 = 3$. Since $2 \in A$ and $3 \in A$, the ordered pair $(2, 3)$ is in R.
- If $x = 3$, $y = 3 + 1 = 4$. Since $3 \in A$ and $4 \in A$, the ordered pair $(3, 4)$ is in R.
- If $x = 4$, $y = 4 + 1 = 5$. Since $4 \in A$ and $5 \in A$, the ordered pair $(4, 5)$ is in R.
- If $x = 5$, $y = 5 + 1 = 6$. Since $5 \in A$ and $6 \in A$, the ordered pair $(5, 6)$ is in R.
- If $x = 6$, $y = 6 + 1 = 7$. Since $6 \in A$ but $7 \notin A$, the ordered pair $(6, 7)$ is not in R.
So, the relation R as a set of ordered pairs is R = $\{(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)\}$.
(i) Depict this relation using an arrow diagram.
To depict the relation using an arrow diagram, we draw two ovals representing the set A. We write the elements of A in each oval. Then, for each ordered pair $(x, y)$ in R, we draw an arrow from the element $x$ in the first oval (representing the domain set) to the element $y$ in the second oval (representing the codomain set).
The diagram would show:
- An arrow from 1 to 2.
- An arrow from 2 to 3.
- An arrow from 3 to 4.
- An arrow from 4 to 5.
- An arrow from 5 to 6.
(ii) Write down the domain, codomain and range of R.
The domain of the relation R is the set of all first components of the ordered pairs in R.
From R = $\{(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)\}$, the first components are 1, 2, 3, 4, 5.
Domain of R = $\{1, 2, 3, 4, 5\}$.
The codomain of the relation R is the set to which the second elements of the ordered pairs belong. The relation is defined from A to A, so the codomain is set A itself.
Codomain of R = A = $\{1, 2, 3, 4, 5, 6\}$.
The range of the relation R is the set of all second components of the ordered pairs in R.
From R = $\{(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)\}$, the second components are 2, 3, 4, 5, 6.
Range of R = $\{2, 3, 4, 5, 6\}$.
Example 8: The Fig 2.6 shows a relation between the sets P and Q. Write this relation (i) in set-builder form, (ii) in roster form. What is its domain and range?
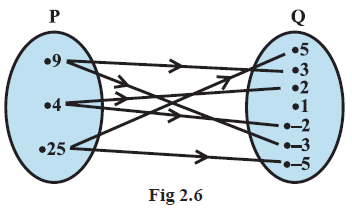
Answer:
Given:
The arrow diagram shows a relation between set P and set Q.
Set P = $\{9, 4, 25\}$
Set Q = $\{5, 3, 2, 1, -2, -3, -5\}$
The arrows indicate the following ordered pairs in the relation R:
- From 9 to 3 and -3.
- From 4 to 2 and -2.
- From 25 to 5 and -5.
To Find:
(i) The relation R in set-builder form.
(ii) The relation R in roster form.
Domain of R and Range of R.
Solution:
From the arrow diagram, the ordered pairs in the relation R are:
- (9, 3)
- (9, -3)
- (4, 2)
- (4, -2)
- (25, 5)
- (25, -5)
(i) Set-builder form:
We observe the relationship between the elements in the ordered pairs $(x, y)$. The first element $x$ is from set P and the second element $y$ is from set Q. We see that the first element is the square of the second element in each pair.
- $9 = 3^2$ and $9 = (-3)^2$
- $4 = 2^2$ and $4 = (-2)^2$
- $25 = 5^2$ and $25 = (-5)^2$
So, the relation can be expressed as $x = y^2$, where $x \in P$ and $y \in Q$.
Therefore, the relation R in set-builder form is:
$R = \{(x, y) : x \in P, y \in Q, x = y^2\}$
(ii) Roster form:
The roster form of the relation is the set of all ordered pairs identified from the arrow diagram.
$R = \{(9, 3), (9, -3), (4, 2), (4, -2), (25, 5), (25, -5)\}$
Domain of R:
The domain of the relation R is the set of all first components of the ordered pairs in R.
Domain of R = $\{9, 4, 25\}$
Range of R:
The range of the relation R is the set of all second components of the ordered pairs in R.
Range of R = $\{3, -3, 2, -2, 5, -5\}$
Arranging in increasing order, the range is: $\{-5, -3, -2, 2, 3, 5\}$
Example 9: Let A = {1, 2} and B = {3, 4}. Find the number of relations from A to B.
Answer:
Given:
Set A = $\{1, 2\}$
Set B = $\{3, 4\}$
To Find:
The number of relations from A to B.
Solution:
A relation from set A to set B is defined as any subset of the Cartesian product A $\times$ B.
First, we need to find the number of elements in set A and set B.
The number of elements in set A is $|A| = 2$.
The number of elements in set B is $|B| = 2$.
Next, we find the number of elements in the Cartesian product A $\times$ B.
The number of elements in A $\times$ B is given by $|A \times B| = |A| \times |B|$.
$|A \times B| = 2 \times 2$
$|A \times B| = 4$
The set A $\times$ B has 4 elements. These elements are the ordered pairs: $\{(1, 3), (1, 4), (2, 3), (2, 4)\}$.
The number of relations from A to B is equal to the number of subsets of A $\times$ B.
The number of subsets of a set with $m$ elements is $2^m$.
In this case, the set A $\times$ B has 4 elements ($m = 4$).
So, the number of subsets of A $\times$ B is $2^4$.
Number of relations = $2^4$
Number of relations = $16$
Therefore, the number of relations from set A to set B is 16.
Exercise 2.2
Question 1. Let A = {1, 2, 3,...,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
Answer:
Given:
Set A = $\{1, 2, 3, ..., 14\}$.
Relation R from A to A defined by R = $\{(x, y) : 3x – y = 0, \text{ where } x, y \in A\}$.
To Find:
The domain, codomain, and range of R.
Solution:
The relation R is defined by the equation $3x – y = 0$, which can be rewritten as $y = 3x$. The ordered pairs $(x, y)$ belonging to the relation R must satisfy this equation, with both $x$ and $y$ being elements of set A = $\{1, 2, 3, ..., 14\}$.
We find the ordered pairs $(x, y)$ by substituting values for $x$ from set A and checking if the resulting $y$ is also in set A.
- If $x = 1$, then $y = 3(1) = 3$. Since $1 \in A$ and $3 \in A$, $(1, 3) \in R$.
- If $x = 2$, then $y = 3(2) = 6$. Since $2 \in A$ and $6 \in A$, $(2, 6) \in R$.
- If $x = 3$, then $y = 3(3) = 9$. Since $3 \in A$ and $9 \in A$, $(3, 9) \in R$.
- If $x = 4$, then $y = 3(4) = 12$. Since $4 \in A$ and $12 \in A$, $(4, 12) \in R$.
- If $x = 5$, then $y = 3(5) = 15$. Since $5 \in A$ but $15 \notin A$ (as $15 > 14$), $(5, 15) \notin R$.
For any value of $x$ greater than 4 in set A, the corresponding value of $y = 3x$ will be greater than 14 and thus not in set A. Therefore, we have found all ordered pairs in the relation R.
The relation R in roster form is R = $\{(1, 3), (2, 6), (3, 9), (4, 12)\}$.
The domain of the relation R is the set of all first components of the ordered pairs in R.
Domain of R = $\{1, 2, 3, 4\}$.
The codomain of the relation R is the set to which the second elements of the ordered pairs belong. Since the relation is defined from A to A, the codomain is set A itself.
Codomain of R = A = $\{1, 2, 3, ..., 14\}$.
The range of the relation R is the set of all second components of the ordered pairs in R.
Range of R = $\{3, 6, 9, 12\}$.
Question 2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
Answer:
Given:
The set of natural numbers N = $\{1, 2, 3, ...\}$.
Relation R on N defined by R = $\{(x, y) : y = x + 5, x \text{ is a natural number less than 4; } x, y \in N\}$.
To Find:
The relation R in roster form.
The domain of R.
The range of R.
The codomain of R.
Solution:
The relation R is defined by the rule $y = x + 5$. The values for $x$ are restricted to natural numbers less than 4, which are 1, 2, and 3. Both $x$ and the resulting $y$ must be natural numbers ($x, y \in N$).
Let's find the ordered pairs $(x, y)$ that belong to the relation R:
- If $x = 1$, then $y = 1 + 5 = 6$. Since $1 \in N$ and $6 \in N$, the ordered pair $(1, 6)$ is in R.
- If $x = 2$, then $y = 2 + 5 = 7$. Since $2 \in N$ and $7 \in N$, the ordered pair $(2, 7)$ is in R.
- If $x = 3$, then $y = 3 + 5 = 8$. Since $3 \in N$ and $8 \in N$, the ordered pair $(3, 8)$ is in R.
For any other natural number $x \ge 4$, the condition "$x$ is a natural number less than 4" is not met.
Thus, the relation R in roster form is:
R = {(1, 6), (2, 7), (3, 8)}.
The domain of the relation R is the set of all first components of the ordered pairs in R.
Domain of R = $\{1, 2, 3\}$.
The codomain of the relation R is the set on which the relation is defined for the second elements. The relation is defined on the set N of natural numbers.
Codomain of R = N = $\{1, 2, 3, 4, ...\}$.
The range of the relation R is the set of all second components of the ordered pairs in R.
Range of R = $\{6, 7, 8\}$.
Question 3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
Answer:
Given:
Set A = $\{1, 2, 3, 5\}$
Set B = $\{4, 6, 9\}$
Relation R from A to B defined by R = $\{(x, y) : \text{the difference between x and y is odd; } x \in A, y \in B\}$.
To Find:
The relation R in roster form.
Solution:
The relation R consists of ordered pairs $(x, y)$ such that $x \in A$, $y \in B$, and the difference between $x$ and $y$ is an odd number. The difference between $x$ and $y$ being odd means $|x - y|$ is an odd number.
Recall that the difference between two integers is odd if and only if one integer is odd and the other integer is even.
We need to find pairs $(x, y)$ where $x \in A$ and $y \in B$ such that one of $x$ and $y$ is odd and the other is even.
Elements of A: Odd numbers are $\{1, 3, 5\}$, Even numbers are $\{2\}$.
Elements of B: Odd number is $\{9\}$, Even numbers are $\{4, 6\}$.
We form the pairs $(x, y)$ where $x \in A$ and $y \in B$ such that $x$ and $y$ have different parity:
- If $x$ is odd (from A) and $y$ is even (from B):
- $x=1$, $y=4 \implies |1-4|=3$ (odd). Pair: $(1, 4)$.
- $x=1$, $y=6 \implies |1-6|=5$ (odd). Pair: $(1, 6)$.
- $x=3$, $y=4 \implies |3-4|=1$ (odd). Pair: $(3, 4)$.
- $x=3$, $y=6 \implies |3-6|=3$ (odd). Pair: $(3, 6)$.
- $x=5$, $y=4 \implies |5-4|=1$ (odd). Pair: $(5, 4)$.
- $x=5$, $y=6 \implies |5-6|=1$ (odd). Pair: $(5, 6)$.
- If $x$ is even (from A) and $y$ is odd (from B):
- $x=2$, $y=9 \implies |2-9|=7$ (odd). Pair: $(2, 9)$.
Combining all the ordered pairs that satisfy the condition, we get the relation R in roster form:
R = {(1, 4), (1, 6), (3, 4), (3, 6), (5, 4), (5, 6), (2, 9)}.
Question 4. The Fig 2.7 shows a relationship between the sets P and Q. Write this relation
(i) in set-builder form
(ii) roster form.
What is its domain and range?

Answer:
Given:
The arrow diagram shows a relation from set P to set Q.
Set P = $\{5, 6, 7\}$
Set Q = $\{3, 4, 5\}$
The relation R is indicated by the arrows from elements in P to elements in Q.
To Find:
(i) Relation R in set-builder form.
(ii) Relation R in roster form.
Domain of R.
Range of R.
Solution:
(ii) Relation R in roster form:
The arrows in the diagram represent the ordered pairs $(x, y)$ in the relation R, where the arrow goes from $x \in P$ to $y \in Q$. Listing the pairs corresponding to the arrows:
- Arrow from 5 to 3 corresponds to the ordered pair $(5, 3)$.
- Arrow from 6 to 4 corresponds to the ordered pair $(6, 4)$.
- Arrow from 7 to 5 corresponds to the ordered pair $(7, 5)$.
Therefore, the relation R in roster form is:
$R = \{(5, 3), (6, 4), (7, 5)\}$
(i) Relation R in set-builder form:
We need to find a rule that relates the first element $x$ to the second element $y$ for all ordered pairs $(x, y)$ in the relation R. Let's examine the pairs:
- For $(5, 3)$, we have $5 - 2 = 3$.
- For $(6, 4)$, we have $6 - 2 = 4$.
- For $(7, 5)$, we have $7 - 2 = 5$.
The rule is that the second element $y$ is 2 less than the first element $x$. This can be written as $y = x - 2$ or $x - y = 2$. Also, $x$ must be an element of set P, and $y$ must be an element of set Q.
Therefore, the relation R in set-builder form is:
$R = \{(x, y) : x \in P, y \in Q, y = x - 2\}$
or equivalently,
$R = \{(x, y) : x \in P, y \in Q, x - y = 2\}$
Domain of R:
The domain of the relation R is the set of all first components of the ordered pairs in R.
From $R = \{(5, 3), (6, 4), (7, 5)\}$, the first components are 5, 6, and 7.
Domain of R = $\{5, 6, 7\}$. This is equal to set P.
Range of R:
The range of the relation R is the set of all second components of the ordered pairs in R.
From $R = \{(5, 3), (6, 4), (7, 5)\}$, the second components are 3, 4, and 5.
Range of R = $\{3, 4, 5\}$. This is equal to set Q.
Question 5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b ∈ A, b is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
Answer:
Given:
Set A = $\{1, 2, 3, 4, 6\}$.
Relation R on A defined by R = $\{(a, b) : a, b \in A, \text{ b is exactly divisible by a}\}$.
The condition "b is exactly divisible by a" means that $a$ is a factor of $b$, or $\frac{b}{a}$ is an integer with no remainder.
To Find:
(i) Relation R in roster form.
(ii) Domain of R.
(iii) Range of R.
Solution:
(i) Write R in roster form
We need to find all ordered pairs $(a, b)$ such that both $a$ and $b$ are in set A, and $b$ is exactly divisible by $a$. We can systematically check each possible value of $a$ from set A and find the values of $b$ from set A that are divisible by $a$.
- If $a = 1$: $b$ is divisible by 1 for all $b \in A$. Pairs: $(1, 1), (1, 2), (1, 3), (1, 4), (1, 6)$.
- If $a = 2$: $b \in A$ is divisible by 2. The elements in A divisible by 2 are 2, 4, 6. Pairs: $(2, 2), (2, 4), (2, 6)$.
- If $a = 3$: $b \in A$ is divisible by 3. The elements in A divisible by 3 are 3, 6. Pairs: $(3, 3), (3, 6)$.
- If $a = 4$: $b \in A$ is divisible by 4. The only element in A divisible by 4 is 4. Pair: $(4, 4)$.
- If $a = 6$: $b \in A$ is divisible by 6. The only element in A divisible by 6 is 6. Pair: $(6, 6)$.
Combining all the ordered pairs, the relation R in roster form is:
R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}.
(ii) Find the domain of R
The domain of the relation R is the set of all first components of the ordered pairs in R.
From R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}, the first components are 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 6. The set of unique first components is $\{1, 2, 3, 4, 6\}$.
Domain of R = {1, 2, 3, 4, 6}.
This is equal to set A, which means that the relation starts from every element in A.
(iii) Find the range of R
The range of the relation R is the set of all second components of the ordered pairs in R.
From R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}, the second components are 1, 2, 3, 4, 6, 2, 4, 6, 3, 6, 4, 6. The set of unique second components is $\{1, 2, 3, 4, 6\}$.
Range of R = {1, 2, 3, 4, 6}.
In this case, the range of R is also equal to set A. Since the relation is on A, the codomain is also A.
Question 6. Determine the domain and range of the relation R defined by R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}.
Answer:
Given:
The relation R is defined by R = $\{(x, x + 5) : x \in \{0, 1, 2, 3, 4, 5\}\}$.
To Find:
The domain of R.
The range of R.
Solution:
The relation R consists of ordered pairs $(x, y)$ where the first element $x$ is taken from the set $\{0, 1, 2, 3, 4, 5\}$, and the second element $y$ is determined by the rule $y = x + 5$.
Let's list the ordered pairs in the relation R by substituting each value of $x$ from the given set:
- If $x = 0$, then $y = 0 + 5 = 5$. The ordered pair is $(0, 5)$.
- If $x = 1$, then $y = 1 + 5 = 6$. The ordered pair is $(1, 6)$.
- If $x = 2$, then $y = 2 + 5 = 7$. The ordered pair is $(2, 7)$.
- If $x = 3$, then $y = 3 + 5 = 8$. The ordered pair is $(3, 8)$.
- If $x = 4$, then $y = 4 + 5 = 9$. The ordered pair is $(4, 9)$.
- If $x = 5$, then $y = 5 + 5 = 10$. The ordered pair is $(5, 10)$.
So, the relation R in roster form is R = $\{(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)\}$.
The domain of the relation R is the set of all first components of the ordered pairs in R.
From R = $\{(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)\}$, the first components are 0, 1, 2, 3, 4, 5.
Domain of R = {0, 1, 2, 3, 4, 5}.
The range of the relation R is the set of all second components of the ordered pairs in R.
From R = $\{(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)\}$, the second components are 5, 6, 7, 8, 9, 10.
Range of R = {5, 6, 7, 8, 9, 10}.
Question 7. Write the relation R = {(x, x3) : x is a prime number less than 10} in roster form.
Answer:
Given:
The relation R is defined by R = $\{(x, x^3) : x \text{ is a prime number less than 10}\}$.
To Find:
The relation R in roster form.
Solution:
The relation R consists of ordered pairs $(x, y)$ where $y = x^3$, and $x$ is a prime number less than 10.
First, we identify the prime numbers less than 10.
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Prime numbers less than 10 are 2, 3, 5, and 7.
Now, we find the corresponding value of $y = x^3$ for each of these prime numbers:
- If $x = 2$, then $y = 2^3 = 2 \times 2 \times 2 = 8$. The ordered pair is $(2, 8)$.
- If $x = 3$, then $y = 3^3 = 3 \times 3 \times 3 = 27$. The ordered pair is $(3, 27)$.
- If $x = 5$, then $y = 5^3 = 5 \times 5 \times 5 = 125$. The ordered pair is $(5, 125)$.
- If $x = 7$, then $y = 7^3 = 7 \times 7 \times 7 = 343$. The ordered pair is $(7, 343)$.
So, the relation R in roster form is:
R = {(2, 8), (3, 27), (5, 125), (7, 343)}.
Optional: Domain and Range (though not explicitly asked, it's good practice)
Domain of R = $\{2, 3, 5, 7\}$ (the set of prime numbers less than 10).
Range of R = $\{8, 27, 125, 343\}$ (the set of cubes of these prime numbers).
Question 8. Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Answer:
Given:
Set A = $\{x, y, z\}$
Set B = $\{1, 2\}$
To Find:
The number of relations from A to B.
Solution:
A relation R from set A to set B is defined as any subset of the Cartesian product A $\times$ B.
To find the number of relations from A to B, we first need to find the number of elements in the Cartesian product A $\times$ B.
The number of elements in set A is $|A| = 3$.
The number of elements in set B is $|B| = 2$.
The number of elements in the Cartesian product A $\times$ B is given by the product of the number of elements in A and the number of elements in B.
$|A \times B| = |A| \times |B|$
$|A \times B| = 3 \times 2$
$|A \times B| = 6$
The set A $\times$ B has 6 elements. These elements are the ordered pairs: $\{(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)\}$.
The number of relations from A to B is equal to the number of subsets of A $\times$ B.
The number of subsets of a set with $m$ elements is $2^m$.
In this case, the set A $\times$ B has 6 elements ($m = 6$).
So, the number of subsets of A $\times$ B is $2^6$.
Number of relations = $2^6$
Calculate $2^6$:
$2^6 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 4 \times 4 \times 4 = 16 \times 4 = 64$.
Number of relations = $64$
Therefore, the number of relations from set A to set B is 64.
Question 9. Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
Answer:
Given:
The relation R is defined on the set of integers Z.
R = $\{(a, b) : a, b \in Z, \text{ a – b is an integer}\}$.
The set of integers $Z = \{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\}$.
To Find:
The domain of R.
The range of R.
Solution:
The relation R consists of all ordered pairs $(a, b)$ such that $a$ and $b$ are both integers ($a \in Z, b \in Z$), and the difference $a - b$ is also an integer.
Let's consider the condition "$a - b$ is an integer". We know that the difference between any two integers is always an integer.
For any choice of $a \in Z$ and any choice of $b \in Z$, the result of $a - b$ will necessarily be an integer.
This means that the condition "$a - b$ is an integer" is true for all possible pairs of integers $(a, b)$.
Therefore, the relation R includes every ordered pair $(a, b)$ where $a$ is an integer and $b$ is an integer.
The relation R is the entire Cartesian product of Z with itself.
$R = \{(a, b) : a \in Z, b \in Z\} = Z \times Z$.
The domain of a relation is the set of all first components of the ordered pairs in the relation.
For the relation R = Z $\times$ Z, the first component '$a$' can be any element from the first set, which is Z.
Domain of R = $\{a \mid (a, b) \in R \text{ for some } b \in Z\}$.
Since $(a, b) \in Z \times Z$ for all $a \in Z$ and $b \in Z$, any integer $a$ can be the first component of an ordered pair in R (e.g., $(a, 0) \in R$ because $a \in Z, 0 \in Z,$ and $a-0=a \in Z$).
So, the set of all first components is Z.
Domain of R = Z.
The range of a relation is the set of all second components of the ordered pairs in the relation.
For the relation R = Z $\times$ Z, the second component '$b$' can be any element from the second set, which is Z.
Range of R = $\{b \mid (a, b) \in R \text{ for some } a \in Z\}$.
Since $(a, b) \in Z \times Z$ for all $a \in Z$ and $b \in Z$, any integer $b$ can be the second component of an ordered pair in R (e.g., $(0, b) \in R$ because $0 \in Z, b \in Z,$ and $0-b=-b \in Z$).
So, the set of all second components is Z.
Range of R = Z.
The codomain of R is also Z, as the relation is defined from Z to Z.
Example 10 to 17 (Before Exercise 2.3)
Example 10: Let N be the set of natural numbers and the relation R be defined on N such that R = {(x, y) : y = 2x, x, y ∈ N}.
What is the domain, codomain and range of R? Is this relation a function?
Answer:
Given:
The set of natural numbers N = $\{1, 2, 3, ...\}$.
The relation R is defined on N such that R = $\{(x, y) : y = 2x, \text{ where } x \in N \text{ and } y \in N\}$.
To Find:
The domain of R.
The codomain of R.
The range of R.
Whether R is a function.
Solution:
The relation R consists of ordered pairs $(x, y)$ where $x$ is a natural number, and $y$ is obtained by multiplying $x$ by 2. The resulting $y$ must also be a natural number.
Let's list some elements of the relation R by substituting values for $x$ from N:
- If $x = 1$, $y = 2(1) = 2$. Since $1 \in N$ and $2 \in N$, $(1, 2) \in R$.
- If $x = 2$, $y = 2(2) = 4$. Since $2 \in N$ and $4 \in N$, $(2, 4) \in R$.
- If $x = 3$, $y = 2(3) = 6$. Since $3 \in N$ and $6 \in N$, $(3, 6) \in R$.
- If $x = 4$, $y = 2(4) = 8$. Since $4 \in N$ and $8 \in N$, $(4, 8) \in R$.
- And so on... for every natural number $x$.
So, R = $\{(1, 2), (2, 4), (3, 6), (4, 8), \dots\}$.
The domain of the relation R is the set of all first components of the ordered pairs in R.
From the definition R = $\{(x, 2x) : x \in N\}$, the first components are all possible values of $x$, which are the elements of the set N.
Domain of R = N = {1, 2, 3, ...}.
The codomain of the relation R is the set to which the second elements of the ordered pairs belong. The relation is defined "on N", which means it is a relation from N to N. Thus, the codomain is the set N.
Codomain of R = N = {1, 2, 3, ...}.
The range of the relation R is the set of all second components of the ordered pairs in R.
The second components are given by $y = 2x$, where $x \in N$. Substituting values for $x$, we get $2(1)=2, 2(2)=4, 2(3)=6, \dots$
The range consists of all even natural numbers.
Range of R = {2, 4, 6, 8, ...}.
Is this relation a function?
A relation R from a set A to a set B is called a function if every element in set A has one and only one image in set B under the relation R.
In this relation R, the domain is N (the set of natural numbers from which $x$ is taken), and the codomain is N (the set of natural numbers where $y$ must belong).
For each element $x$ in the domain N, the rule $y = 2x$ gives a unique value for $y$. Since $x$ is a natural number, $2x$ is also a natural number, so $y \in N$.
For example:
- For $x=1$, $y=2$. There is only one image (2) for the element 1.
- For $x=5$, $y=10$. There is only one image (10) for the element 5.
- For any unique natural number $x$, the value $2x$ is a unique natural number.
Since every element in the domain N has exactly one image in the codomain N under the relation R, the relation R is a function.
Yes, this relation is a function.
Example 11: Examine each of the following relations given below and state in each case, giving reasons whether it is a function or not?
(i) R = {(2,1), (3,1), (4,2)},
(ii) R = {(2,2), (2,4), (3,3), (4,4)}
(iii) R = {(1,2), (2,3), (3,4), (4,5), (5,6), (6,7)}
Answer:
Recall the definition of a function: A relation R from a set A to a set B is called a function if every element in set A has one and only one image in set B under the relation R. Equivalently, for a relation to be a function, no two distinct ordered pairs in the relation can have the same first element.
(i) R = {(2,1), (3,1), (4,2)}
The domain of this relation is the set of first components: {2, 3, 4}.
Let's check if each element in the domain has a unique image (second component):
- The element 2 is related only to 1 (its image is 1).
- The element 3 is related only to 1 (its image is 1).
- The element 4 is related only to 2 (its image is 2).
Each element in the domain {2, 3, 4} has exactly one image in the range {1, 2}. Although elements 2 and 3 share the same image (1), this is permissible for a function; the requirement is that each element in the domain has *only one* image.
Therefore, this relation is a function.
(ii) R = {(2,2), (2,4), (3,3), (4,4)}
The domain of this relation is the set of first components: {2, 3, 4}.
Let's check the images of the elements in the domain:
- The element 2 is related to 2 (image is 2) and also related to 4 (image is 4).
Since the element 2 in the domain has two distinct images (2 and 4), this relation violates the condition for being a function.
Therefore, this relation is not a function.
(iii) R = {(1,2), (2,3), (3,4), (4,5), (5,6), (6,7)}
The domain of this relation is the set of first components: {1, 2, 3, 4, 5, 6}.
Let's check the images of the elements in the domain:
- The element 1 is related only to 2 (image is 2).
- The element 2 is related only to 3 (image is 3).
- The element 3 is related only to 4 (image is 4).
- The element 4 is related only to 5 (image is 5).
- The element 5 is related only to 6 (image is 6).
- The element 6 is related only to 7 (image is 7).
Each element in the domain {1, 2, 3, 4, 5, 6} has exactly one image in the range {2, 3, 4, 5, 6, 7}. There are no two distinct ordered pairs with the same first element.
Therefore, this relation is a function.
Example 12: Let N be the set of natural numbers. Define a real valued function f : N → N by f (x) = 2x + 1. Using this definition, complete the table given below.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| y | f(1)=... | f(2)=... | f(3)=... | f(4)=... | f(5)=... | f(6)=... | f(7)=... |
Answer:
Given:
Set of natural numbers N = $\{1, 2, 3, ...\}$.
A real valued function $f: N \to N$ defined by $f(x) = 2x + 1$.
The table provides values of $x$ for which $f(x)$ needs to be calculated.
To Complete:
The given table by finding the values of $f(x)$ for $x \in \{1, 2, 3, 4, 5, 6, 7\}$.
Solution:
The function is defined as $f(x) = 2x + 1$. To complete the table, we substitute the given values of $x$ into the function rule and find the corresponding value of $f(x)$.
For $x = 1$: $f(1) = 2(1) + 1 = 2 + 1 = 3$.
For $x = 2$: $f(2) = 2(2) + 1 = 4 + 1 = 5$.
For $x = 3$: $f(3) = 2(3) + 1 = 6 + 1 = 7$.
For $x = 4$: $f(4) = 2(4) + 1 = 8 + 1 = 9$.
For $x = 5$: $f(5) = 2(5) + 1 = 10 + 1 = 11$.
For $x = 6$: $f(6) = 2(6) + 1 = 12 + 1 = 13$.
For $x = 7$: $f(7) = 2(7) + 1 = 14 + 1 = 15$.
We can now complete the table:
| x | y = f(x) = $2x + 1$ |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| 7 | 15 |
Example 13: Define the function f: R → R by y = f(x) = x2 , x ∈ R. Complete the Table given below by using this definition. What is the domain and range of this function? Draw the graph of f.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| y = f(x) = x2 |
Answer:
Given:
The function $f: R \to R$ defined by $y = f(x) = x^2$, where $x \in R$.
A table with specific values of $x$ for which $f(x)$ needs to be calculated.
To Find:
Complete the given table.
Determine the domain of the function $f$.
Determine the range of the function $f$.
Draw the graph of the function $f$.
Solution:
The function is defined by $f(x) = x^2$. We calculate the value of $f(x)$ for each given value of $x$ by squaring the $x$ value.
- For $x = -4$, $f(-4) = (-4)^2 = 16$.
- For $x = -3$, $f(-3) = (-3)^2 = 9$.
- For $x = -2$, $f(-2) = (-2)^2 = 4$.
- For $x = -1$, $f(-1) = (-1)^2 = 1$.
- For $x = 0$, $f(0) = (0)^2 = 0$.
- For $x = 1$, $f(1) = (1)^2 = 1$.
- For $x = 2$, $f(2) = (2)^2 = 4$.
- For $x = 3$, $f(3) = (3)^2 = 9$.
- For $x = 4$, $f(4) = (4)^2 = 16$.
Completing the table with the calculated values:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y = f(x) = $x^2$ | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
Domain of f:
The domain of a function $f: A \to B$ is the set A from which the input values ($x$) are taken. The problem states that the function is defined for $x \in R$, where R is the set of all real numbers.
Therefore, the domain of the function $f(x) = x^2$ is the set of all real numbers.
Domain of $f = R = (-\infty, \infty)$.
Range of f:
The range of a function is the set of all possible output values ($y$ or $f(x)$) for the given domain. The function is $f(x) = x^2$. For any real number $x$, its square $x^2$ is always greater than or equal to zero ($x^2 \ge 0$).
The smallest value of $x^2$ occurs when $x=0$, where $f(0)=0$. As $x$ takes any real value (positive or negative), $x^2$ takes all non-negative real values.
Therefore, the range of the function $f(x) = x^2$ is the set of all non-negative real numbers.
Range of $f = [0, \infty)$.
Graph of f:
To draw the graph of $f(x) = x^2$, we plot the ordered pairs $(x, f(x))$ from the table and for other real values of $x$ on a Cartesian coordinate plane. The table gives us several points on the graph:
$(-4, 16), (-3, 9), (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4), (3, 9), (4, 16)$.
The graph of $y = x^2$ is a parabola that opens upwards, with its vertex at the origin $(0, 0)$. It is symmetric with respect to the y-axis.
To draw the graph:
1. Draw the x-axis and the y-axis.
2. Plot the points obtained from the table: $(-4, 16), (-3, 9), (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4), (3, 9), (4, 16)$.
3. Draw a smooth curve passing through these points. The curve should start from the upper left, go down to the vertex at $(0, 0)$, and then go up towards the upper right.
The resulting curve is the graph of $f(x) = x^2$.
Example 14: Draw the graph of the function f : R → R defined by f (x) = x3 , x ∈ R.
Answer:
Given:
The function $f : R \to R$ defined by $f(x) = x^3$, where $x \in R$.
To Draw:
The graph of the function $f(x) = x^3$.
Solution:
The function is given by $f(x) = x^3$. To draw the graph of this function, we can compute the values of $y = f(x)$ for some selected values of $x$ and plot the corresponding points $(x, y)$ on a Cartesian plane.
Let's choose some integer values for $x$ and calculate the corresponding values of $f(x)$:
| x | f(x) = $x^3$ | Point (x, f(x)) |
| -2 | $(-2)^3 = -8$ | (-2, -8) |
| -1 | $(-1)^3 = -1$ | (-1, -1) |
| 0 | $(0)^3 = 0$ | (0, 0) |
| 1 | $(1)^3 = 1$ | (1, 1) |
| 2 | $(2)^3 = 8$ | (2, 8) |
The points we can plot are (-2, -8), (-1, -1), (0, 0), (1, 1), and (2, 8).
The graph of $y = x^3$ is a smooth curve. It passes through the origin (0, 0). As $x$ increases, $y$ also increases. For positive values of $x$, $y$ is positive and increases rapidly. For negative values of $x$, $y$ is negative and decreases rapidly (becomes more negative).
To draw the graph:
1. Draw the horizontal x-axis and the vertical y-axis.
2. Plot the points from the table, such as (-2, -8), (-1, -1), (0, 0), (1, 1), and (2, 8).
3. Draw a smooth curve that passes through these plotted points. Extend the curve beyond these points to show that the domain is all real numbers.
The resulting curve starts from the bottom-left, passes through the origin, and extends towards the top-right. The graph is symmetric with respect to the origin.
The domain of the function $f(x) = x^3$ is given as R, the set of all real numbers.
Domain of $f = R = (-\infty, \infty)$.
The range of the function $f(x) = x^3$ is also R, the set of all real numbers, because any real number $y$ can be expressed as the cube of some real number $x$ (i.e., $x = \sqrt[3]{y}$).
Range of $f = R = (-\infty, \infty)$.
Example 15: Define the real valued function f : R – {0} → R defined by f(x) = $\frac{1}{x}$ , x ∈ R – {0}. Complete the Table given below using this definition. What is the domain and range of this function?
| x | -2 | -1.5 | -1 | -0.5 | 0.25 | 0.5 | 1 | 1.5 | 2 |
|---|---|---|---|---|---|---|---|---|---|
| $y = \frac{1}{x}$ | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Answer:
Given:
The real valued function $f : R – \{0\} \to R$ defined by $f(x) = \frac{1}{x}$, where $x \in R – \{0\}$.
A table with specific values of $x$ for which $y = f(x)$ needs to be calculated.
To Find:
Complete the given table.
Determine the domain of the function $f$.
Determine the range of the function $f$.
Solution:
The function is defined by $f(x) = \frac{1}{x}$. We calculate the value of $y = f(x)$ for each given value of $x$ by taking the reciprocal of $x$.
- For $x = -2$, $y = f(-2) = \frac{1}{-2} = -0.5$.
- For $x = -1.5$, $y = f(-1.5) = \frac{1}{-1.5} = \frac{1}{-3/2} = -\frac{2}{3}$.
- For $x = -1$, $y = f(-1) = \frac{1}{-1} = -1$.
- For $x = -0.5$, $y = f(-0.5) = \frac{1}{-0.5} = \frac{1}{-1/2} = -2$.
- For $x = 0.25$, $y = f(0.25) = \frac{1}{0.25} = \frac{1}{1/4} = 4$.
- For $x = 0.5$, $y = f(0.5) = \frac{1}{0.5} = \frac{1}{1/2} = 2$.
- For $x = 1$, $y = f(1) = \frac{1}{1} = 1$.
- For $x = 1.5$, $y = f(1.5) = \frac{1}{1.5} = \frac{1}{3/2} = \frac{2}{3}$.
- For $x = 2$, $y = f(2) = \frac{1}{2} = 0.5$.
Completing the table with the calculated values:
| x | -2 | -1.5 | -1 | -0.5 | 0.25 | 0.5 | 1 | 1.5 | 2 |
| $y = \frac{1}{x}$ | -0.5 | $-\frac{2}{3}$ | -1 | -2 | 4 | 2 | 1 | $\frac{2}{3}$ | 0.5 |
Domain of f:
The domain of a function $f: A \to B$ is the set A from which the input values ($x$) are taken. The problem explicitly defines the domain as $R – \{0\}$. This means the function is defined for all real numbers except 0, because division by zero is undefined.
Therefore, the domain of the function $f(x) = \frac{1}{x}$ is the set of all real numbers except 0.
Domain of $f = R – \{0\}$.
Range of f:
The range of a function is the set of all possible output values ($y$ or $f(x)$) for the given domain. The function is $f(x) = \frac{1}{x}$ with the domain $R – \{0\}$.
We need to find the set of all values that $y = \frac{1}{x}$ can take when $x$ is any non-zero real number.
If $y = \frac{1}{x}$, then $x = \frac{1}{y}$. For $x$ to be a non-zero real number (which it must be as it's in the domain), $y$ cannot be 0 (since division by zero is undefined). Also, for any non-zero real value of $y$, we can find a corresponding non-zero real value of $x$ such that $f(x) = y$.
For example, if $y = 5$, then $x = \frac{1}{5} = 0.2$, and $f(0.2) = \frac{1}{0.2} = 5$. If $y = -0.1$, then $x = \frac{1}{-0.1} = -10$, and $f(-10) = \frac{1}{-10} = -0.1$.
Thus, the function $f(x) = \frac{1}{x}$ can produce any real number as an output, except for 0.
Therefore, the range of the function $f(x) = \frac{1}{x}$ is the set of all real numbers except 0.
Range of $f = R – \{0\}$.
Graph of f:
To draw the graph of $f(x) = \frac{1}{x}$, we plot the ordered pairs $(x, f(x))$ from the table and for other real values of $x$ (excluding $x=0$). The points from the table are approximately: $(-2, -0.5)$, $(-1.5, -0.67)$, $(-1, -1)$, $(-0.5, -2)$, $(0.25, 4)$, $(0.5, 2)$, $(1, 1)$, $(1.5, 0.67)$, $(2, 0.5)$.
The graph of $y = \frac{1}{x}$ is a hyperbola with two branches. One branch is in the first quadrant (where $x > 0$ and $y > 0$), and the other branch is in the third quadrant (where $x < 0$ and $y < 0$).
The x-axis and the y-axis are asymptotes to the graph, meaning the curve gets infinitely close to these axes but never touches them.
To draw the graph:
1. Draw the horizontal x-axis and the vertical y-axis.
2. Plot the points from the table and other points for better accuracy.
3. Draw a smooth curve through the points in the first quadrant, approaching the x-axis as $x$ gets very large and approaching the y-axis as $x$ gets close to 0 from the positive side.
4. Draw a smooth curve through the points in the third quadrant, approaching the x-axis as $x$ gets very small (large negative) and approaching the y-axis as $x$ gets close to 0 from the negative side.
Example 16: Let f(x) = x2 and g(x) = 2x + 1 be two real functions.Find
(f + g) (x), (f – g) (x), (fg) (x), $\left( \frac{f}{g} \right)$ (x).
Answer:
Given:
Two real functions $f(x) = x^2$ and $g(x) = 2x + 1$.
Both functions are defined for all real numbers, so their domains are $R$.
To Find:
The sum function $(f + g) (x)$.
The difference function $(f – g) (x)$.
The product function $(fg) (x)$.
The quotient function $\left( \frac{f}{g} \right)$ (x).
Solution:
The operations on real functions are defined as follows:
1. Sum of functions (f + g)(x):
$(f + g)(x) = f(x) + g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(f + g)(x) = x^2 + (2x + 1)$
$(f + g)(x) = x^2 + 2x + 1$
The domain of $(f + g)(x)$ is the intersection of the domains of $f$ and $g$, which is $R \cap R = R$.
2. Difference of functions (f – g)(x):
$(f – g)(x) = f(x) – g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(f – g)(x) = x^2 - (2x + 1)$
Distribute the negative sign:
$(f – g)(x) = x^2 - 2x - 1$
The domain of $(f – g)(x)$ is the intersection of the domains of $f$ and $g$, which is $R \cap R = R$.
3. Product of functions (fg)(x):
$(fg)(x) = f(x) \cdot g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(fg)(x) = x^2 (2x + 1)$
Distribute $x^2$:
$(fg)(x) = 2x^3 + x^2$
The domain of $(fg)(x)$ is the intersection of the domains of $f$ and $g$, which is $R \cap R = R$.
4. Quotient of functions $\left( \frac{f}{g} \right)$ (x):
$\left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)}$, provided $g(x) \neq 0$.
Substitute the given expressions for $f(x)$ and $g(x)$:
$\left( \frac{f}{g} \right)(x) = \frac{x^2}{2x + 1}$
The domain of $\left( \frac{f}{g} \right)(x)$ is the intersection of the domains of $f$ and $g$, excluding the values of $x$ where $g(x) = 0$.
We need to find the values of $x$ for which $g(x) = 0$:
$2x + 1 = 0$
$2x = -1$
$x = -\frac{1}{2}$
So, the domain of $\left( \frac{f}{g} \right)(x)$ is all real numbers except $-\frac{1}{2}$.
Domain of $\left( \frac{f}{g} \right) = R – \{-\frac{1}{2}\}$.
Summary of results:
$(f + g)(x) = x^2 + 2x + 1$
$(f – g)(x) = x^2 - 2x - 1$
$(fg)(x) = 2x^3 + x^2$
$\left( \frac{f}{g} \right)(x) = \frac{x^2}{2x + 1}$, for $x \neq -\frac{1}{2}$.
Example 17: Let f(x) = $\sqrt{x}$ and g(x) = x be two functions defined over the set of non-negative real numbers. Find (f + g) (x), (f – g) (x), (fg) (x) and $\left( \frac{f}{g} \right)$ (x)
Answer:
Given:
Two real functions $f(x) = \sqrt{x}$ and $g(x) = x$.
Both functions are defined over the set of non-negative real numbers, which is the interval $[0, \infty)$. This is the domain for both functions where their sum, difference, and product are defined.
Domain of $f = [0, \infty)$.
Domain of $g = [0, \infty)$.
To Find:
The sum function $(f + g) (x)$.
The difference function $(f – g) (x)$.
The product function $(fg) (x)$.
The quotient function $\left( \frac{f}{g} \right)$ (x).
Solution:
The operations on real functions are defined as follows:
1. Sum of functions (f + g)(x):
$(f + g)(x) = f(x) + g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(f + g)(x) = \sqrt{x} + x$
The domain of $(f + g)(x)$ is the intersection of the domains of $f$ and $g$, which is $[0, \infty) \cap [0, \infty) = [0, \infty)$.
2. Difference of functions (f – g)(x):
$(f – g)(x) = f(x) – g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(f – g)(x) = \sqrt{x} - x$
The domain of $(f – g)(x)$ is the intersection of the domains of $f$ and $g$, which is $[0, \infty) \cap [0, \infty) = [0, \infty)$.
3. Product of functions (fg)(x):
$(fg)(x) = f(x) \cdot g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(fg)(x) = \sqrt{x} \cdot x$
Using exponent notation, $\sqrt{x} = x^{\frac{1}{2}}$ and $x = x^1$.
$(fg)(x) = x^{\frac{1}{2}} \cdot x^1 = x^{\frac{1}{2} + 1} = x^{\frac{3}{2}}$
The domain of $(fg)(x)$ is the intersection of the domains of $f$ and $g$, which is $[0, \infty) \cap [0, \infty) = [0, \infty)$.
4. Quotient of functions $\left( \frac{f}{g} \right)$ (x):
$\left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)}$, provided the denominator $g(x) \neq 0$.
Substitute the given expressions for $f(x)$ and $g(x)$:
$\left( \frac{f}{g} \right)(x) = \frac{\sqrt{x}}{x}$
The domain of $\left( \frac{f}{g} \right)(x)$ is the intersection of the domains of $f$ and $g$, excluding the values of $x$ where $g(x) = 0$.
Domain of $f$ is $[0, \infty)$. Domain of $g$ is $[0, \infty)$. The intersection is $[0, \infty)$.
We need to find the values of $x$ for which $g(x) = 0$:
$g(x) = x$
So, $g(x) = 0$ when $x = 0$.
Therefore, for the quotient function, the value $x=0$ must be excluded from the domain.
The domain of $\left( \frac{f}{g} \right)(x)$ is $[0, \infty) – \{0\} = (0, \infty)$. This means $x$ cannot be equal to 0.
We can simplify the expression for $\left( \frac{f}{g} \right)(x)$ for $x > 0$:
$\frac{\sqrt{x}}{x} = \frac{x^{\frac{1}{2}}}{x^1} = x^{\frac{1}{2} - 1} = x^{-\frac{1}{2}} = \frac{1}{x^{\frac{1}{2}}} = \frac{1}{\sqrt{x}}$
$\left( \frac{f}{g} \right)(x) = \frac{1}{\sqrt{x}}$
This expression is defined for $x > 0$.
Summary of results:
$(f + g)(x) = \sqrt{x} + x$
$(f – g)(x) = \sqrt{x} - x$
$(fg)(x) = x^{\frac{3}{2}}$
$\left( \frac{f}{g} \right)(x) = \frac{1}{\sqrt{x}}$, for $x \neq 0$.
All functions $(f+g), (f-g), (fg)$ have domain $[0, \infty)$. The function $\left( \frac{f}{g} \right)$ has domain $(0, \infty)$, meaning $x > 0$.
Exercise 2.3
Question 1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}.
Answer:
A relation is a function if and only if every element in its domain is associated with exactly one element in its codomain. In terms of ordered pairs, a relation is a function if no two distinct ordered pairs have the same first element.
(i) R = {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
The first elements of the ordered pairs are 2, 5, 8, 11, 14, and 17.
Each of these first elements appears exactly once in the ordered pairs.
- The first element 2 is associated only with 1.
- The first element 5 is associated only with 1.
- The first element 8 is associated only with 1.
- The first element 11 is associated only with 1.
- The first element 14 is associated only with 1.
- The first element 17 is associated only with 1.
Since every element in the domain (the set of first elements) has a unique image (the second element it is paired with), this relation is a function.
Domain of R: The set of all first elements of the ordered pairs.
Domain of R = $\{2, 5, 8, 11, 14, 17\}$.
Range of R: The set of all second elements of the ordered pairs.
Range of R = $\{1\}$.
(ii) R = {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
The first elements of the ordered pairs are 2, 4, 6, 8, 10, 12, and 14.
Each of these first elements appears exactly once in the ordered pairs.
- The first element 2 is associated only with 1.
- The first element 4 is associated only with 2.
- The first element 6 is associated only with 3.
- The first element 8 is associated only with 4.
- The first element 10 is associated only with 5.
- The first element 12 is associated only with 6.
- The first element 14 is associated only with 7.
Since every element in the domain has a unique image, this relation is a function.
Domain of R: The set of all first elements of the ordered pairs.
Domain of R = $\{2, 4, 6, 8, 10, 12, 14\}$.
Range of R: The set of all second elements of the ordered pairs.
Range of R = $\{1, 2, 3, 4, 5, 6, 7\}$.
(iii) R = {(1, 3), (1, 5), (2, 5)}
The first elements of the ordered pairs are 1 and 2.
The first element 1 appears in two distinct ordered pairs: (1, 3) and (1, 5).
- The first element 1 is associated with 3.
- The first element 1 is also associated with 5.
Since the element 1 in the domain is associated with two different images (3 and 5), this relation violates the condition for being a function.
Therefore, this relation is not a function.
Question 2. Find the domain and range of the following real functions:
(i) f(x) = – |x|
(ii) f(x) = $\sqrt{9 - x^2}$
Answer:
(i) f(x) = – |x|
Domain of f(x) = – |x|:
The domain of a real function is the set of all real numbers for which the function is defined.
The absolute value function $|x|$ is defined for all real numbers $x$. The function $f(x) = -|x|$ involves taking the absolute value of $x$ and then multiplying by -1. Both these operations are defined for all real numbers.
Therefore, the function $f(x) = -|x|$ is defined for all real numbers.
Domain of $f = R = (-\infty, \infty)$.
Range of f(x) = – |x|:
The range of a function is the set of all possible output values. The absolute value of any real number $x$, $|x|$, is always non-negative, i.e., $|x| \ge 0$.
Multiplying by -1 reverses the inequality:
$–|x| \le 0$
So, the value of $f(x) = -|x|$ is always less than or equal to 0.
The maximum value of $-|x|$ is 0, which occurs when $x=0$ (since $|0|=0$, $-|0|=0$). For any other real number $x$, $|x| > 0$, so $-|x| < 0$.
The values of $-|x|$ can be any non-positive real number. For example, to get $-5$, we can use $x=5$ or $x=-5$, since $f(5) = -|5| = -5$ and $f(-5) = -|-5| = -5$.
Thus, the range of the function is the set of all non-positive real numbers.
Range of $f = (-\infty, 0]$.
(ii) f(x) = $\sqrt{9 - x^2}$
Domain of f(x) = $\sqrt{9 - x^2}$:
For a real valued function involving a square root, the expression under the square root sign must be non-negative (greater than or equal to zero), because the square root of a negative number is not a real number.
So, we require $9 - x^2 \ge 0$.
We can rewrite this inequality:
$9 \ge x^2$
Or, $x^2 \le 9$.
Taking the square root of both sides (and considering both positive and negative roots):
$\sqrt{x^2} \le \sqrt{9}$
$|x| \le 3$
This inequality $|x| \le 3$ means that $x$ must be between -3 and 3, inclusive.
$-3 \le x \le 3$
Therefore, the domain of the function is the closed interval [-3, 3].
Domain of $f = [-3, 3]$.
Range of f(x) = $\sqrt{9 - x^2}$:
The range is the set of all possible output values $f(x) = \sqrt{9 - x^2}$ for $x$ in the domain [-3, 3].
Since the square root symbol $\sqrt{\phantom{a}}$ denotes the non-negative square root, the value of $f(x)$ will always be non-negative.
So, $f(x) \ge 0$.
Now let's consider the maximum possible value of $f(x)$. This occurs when the value under the square root, $9 - x^2$, is maximized. Since $x^2 \ge 0$, the maximum value of $9 - x^2$ occurs when $x^2$ is minimized. The minimum value of $x^2$ in the domain [-3, 3] is 0, which occurs when $x=0$.
When $x = 0$, $f(0) = \sqrt{9 - 0^2} = \sqrt{9} = 3$. This is the maximum value of $f(x)$.
When $x = -3$ or $x = 3$, $f(-3) = \sqrt{9 - (-3)^2} = \sqrt{9 - 9} = \sqrt{0} = 0$, and $f(3) = \sqrt{9 - 3^2} = \sqrt{9 - 9} = \sqrt{0} = 0$. These are the minimum values of $f(x)$ in the domain where the square root is defined.
As $x$ varies from -3 to 3, $x^2$ varies from 9 down to 0 and back up to 9. Consequently, $9 - x^2$ varies from 0 up to 9 and back down to 0. The square root $\sqrt{9 - x^2}$ thus varies from $\sqrt{0}=0$ up to $\sqrt{9}=3$ and back down to $\sqrt{0}=0$.
So, the possible values of $f(x)$ are all real numbers from 0 to 3, inclusive.
Range of $f = [0, 3]$.
Question 3. A function f is defined by f(x) = 2x – 5. Write down the values of
(i) f (0),
(ii) f (7),
(iii) f (–3).
Answer:
Given:
The function $f(x) = 2x – 5$.
To Find:
(i) The value of $f(0)$.
(ii) The value of $f(7)$.
(iii) The value of $f(–3)$.
Solution:
The function rule is $f(x) = 2x - 5$. To find the value of the function at a specific input, we substitute that input value for $x$ in the function rule.
(i) f (0):
Substitute $x = 0$ into the function $f(x) = 2x - 5$:
$f(0) = 2(0) - 5$
$f(0) = 0 - 5$
$f(0) = -5$
The value of $f(0)$ is -5.
(ii) f (7):
Substitute $x = 7$ into the function $f(x) = 2x - 5$:
$f(7) = 2(7) - 5$
$f(7) = 14 - 5$
$f(7) = 9$
The value of $f(7)$ is 9.
(iii) f (–3):
Substitute $x = -3$ into the function $f(x) = 2x - 5$:
$f(-3) = 2(-3) - 5$
$f(-3) = -6 - 5$
$f(-3) = -11$
The value of $f(–3)$ is -11.
Question 4. The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = $\frac{9C}{5}$ + 32
Find
(i) t(0)
(ii) t(28)
(iii) t(–10)
(iv) The value of C, when t(C) = 212.
Answer:
Given:
The function $t(C)$ which maps temperature in degrees Celsius ($C$) to temperature in degrees Fahrenheit ($t(C)$) is defined by $t(C) = \frac{9C}{5} + 32$.
To Find:
(i) The value of $t(0)$.
(ii) The value of $t(28)$.
(iii) The value of $t(–10)$.
(iv) The value of $C$ when $t(C) = 212$.
Solution:
The function rule is $t(C) = \frac{9C}{5} + 32$. To find the value of the function for a given temperature in Celsius, we substitute the value of $C$ into the rule.
(i) t(0):
Substitute $C = 0$ into the function $t(C) = \frac{9C}{5} + 32$:
$t(0) = \frac{9(0)}{5} + 32$
$t(0) = 0 + 32$
$t(0) = 32$
This means $0^\circ C$ is equal to $32^\circ F$. The value of $t(0)$ is 32.
(ii) t(28):
Substitute $C = 28$ into the function $t(C) = \frac{9C}{5} + 32$:
$t(28) = \frac{9(28)}{5} + 32$
$t(28) = \frac{252}{5} + 32$
$t(28) = 50.4 + 32$
$t(28) = 82.4$
This means $28^\circ C$ is equal to $82.4^\circ F$. The value of $t(28)$ is 82.4.
(iii) t(–10):
Substitute $C = -10$ into the function $t(C) = \frac{9C}{5} + 32$:
$t(-10) = \frac{9(-10)}{5} + 32$
$t(-10) = \frac{-90}{5} + 32$
$t(-10) = -18 + 32$
$t(-10) = 14$
This means $-10^\circ C$ is equal to $14^\circ F$. The value of $t(–10)$ is 14.
(iv) The value of C, when t(C) = 212:
We are given $t(C) = 212$. We need to find the value of $C$ that satisfies the equation:
$\frac{9C}{5} + 32 = 212$
Subtract 32 from both sides:
$\frac{9C}{5} = 212 - 32$
$\frac{9C}{5} = 180$
Multiply both sides by 5:
$9C = 180 \times 5$
$9C = 900$
Divide both sides by 9:
$C = \frac{900}{9}$
$C = 100$
This means when the temperature is $212^\circ F$, the temperature in Celsius is $100^\circ C$. The value of $C$ when $t(C) = 212$ is 100.
Question 5. Find the range of each of the following functions.
(i) f (x) = 2 – 3x, x ∈ R, x > 0.
(ii) f (x) = x2 + 2, x is a real number.
(iii) f (x) = x, x is a real number.
Answer:
The range of a function is the set of all possible output values ($f(x)$ or $y$) for the given domain.
(i) f (x) = 2 – 3x, x ∈ R, x > 0.
Given Domain: The domain of the function is the set of all real numbers $x$ such that $x > 0$, which can be written as $(0, \infty)$.
Finding the Range: The function is $f(x) = 2 - 3x$. We need to find the set of values that $2 - 3x$ can take when $x > 0$.
Start with the inequality for the domain:
$x > 0$
Multiply the inequality by -3. When multiplying an inequality by a negative number, the direction of the inequality sign reverses:
$-3x < -3(0)$
$-3x < 0$
Now, add 2 to all parts of the inequality:
$2 - 3x < 2 + 0$
$2 - 3x < 2$
Since $f(x) = 2 - 3x$, the inequality $f(x) < 2$ tells us the possible values of $f(x)$.
Thus, the range of the function is the set of all real numbers less than 2, which can be written as $(-\infty, 2)$.
Range of $f = (-\infty, 2)$.
(ii) f (x) = x2 + 2, x is a real number.
Given Domain: The domain of the function is the set of all real numbers, $R = (-\infty, \infty)$.
Finding the Range: The function is $f(x) = x^2 + 2$. We know that for any real number $x$, its square $x^2$ is always non-negative:
$x^2 \ge 0$
Now, add 2 to both sides of the inequality:
$x^2 + 2 \ge 0 + 2$
$x^2 + 2 \ge 2$
Since $f(x) = x^2 + 2$, the inequality $f(x) \ge 2$ tells us that the value of the function is always greater than or equal to 2.
The minimum value of $f(x)$ is 2, which occurs when $x=0$ (since $f(0) = 0^2 + 2 = 2$). As $x$ moves away from 0, $x^2$ increases, and so does $f(x)$.
Thus, the range of the function is the set of all real numbers greater than or equal to 2, which can be written as $[2, \infty)$.
Range of $f = [2, \infty)$.
(iii) f (x) = x, x is a real number.
Given Domain: The domain of the function is the set of all real numbers, $R = (-\infty, \infty)$.
Finding the Range: The function is $f(x) = x$. This is the identity function. For any real number $x$ in the domain, the output $f(x)$ is simply that same real number $x$.
Since $x$ can be any real number, $f(x)$ can also be any real number.
Thus, the range of the function is the set of all real numbers.
Range of $f = R = (-\infty, \infty)$.
Example 18 to 22 - Miscellaneous Examples
Example 18: Let R be the set of real numbers. Define the real function
f: R → R by f(x) = x + 10
and sketch the graph of this function.
Answer:
Given:
The real function $f: R \to R$ defined by $f(x) = x + 10$.
The domain of the function is R (the set of all real numbers).
The codomain of the function is R (the set of all real numbers).
To Sketch:
The graph of the function $f(x) = x + 10$.
Solution:
The function $f(x) = x + 10$ is a linear function of the form $y = mx + c$, where $m$ is the slope and $c$ is the y-intercept. In this case, $y = 1 \cdot x + 10$, so the slope $m = 1$ and the y-intercept $c = 10$. The graph of a linear function is a straight line.
To sketch the graph of a straight line, we need to find at least two points that lie on the line. We can choose any values for $x$ from the domain R and calculate the corresponding value of $y = f(x)$.
Let's choose a few simple values for $x$:
- If $x = 0$, then $y = f(0) = 0 + 10 = 10$. The point is $(0, 10)$. This is the y-intercept.
- If $x = -10$, then $y = f(-10) = -10 + 10 = 0$. The point is $(-10, 0)$. This is the x-intercept.
- If $x = 2$, then $y = f(2) = 2 + 10 = 12$. The point is $(2, 12)$.
We can use any two of these points to draw the line. For example, using $(0, 10)$ and $(-10, 0)$ is convenient as they are the intercepts.
| x | f(x) = x + 10 | Point (x, f(x)) |
| 0 | 10 | (0, 10) |
| -10 | 0 | (-10, 0) |
| 2 | 12 | (2, 12) |
To sketch the graph:
1. Draw the horizontal x-axis and the vertical y-axis, intersecting at the origin (0, 0).
2. Label the axes. Choose an appropriate scale for both axes.
3. Plot at least two points from the table, for example, $(0, 10)$ and $(-10, 0)$.
4. Draw a straight line passing through these plotted points. Extend the line indefinitely in both directions, indicated by arrows, to show that the domain is all real numbers.
The graph is a straight line with a positive slope ($m=1$), crossing the y-axis at $(0, 10)$ and the x-axis at $(-10, 0)$.
The domain of the function $f(x) = x + 10$ is given as R, the set of all real numbers, as the expression $x+10$ is defined for all real values of $x$.
Domain of $f = R = (-\infty, \infty)$.
The range of the function $f(x) = x + 10$ is the set of all possible output values ($y$ or $f(x)$). Since for every real number $y$, we can find a real number $x = y - 10$ such that $f(x) = (y-10) + 10 = y$, the function can take any real value.
Range of $f = R = (-\infty, \infty)$.
Example 19: Let R be a relation from Q to Q defined by R = {(a,b): a,b ∈ Q and a – b ∈ Z}. Show that
(i) (a, a) ∈ R for all a ∈ Q
(ii) (a, b) ∈ R implies that (b, a) ∈ R
(iii) (a, b) ∈ R and (b,c) ∈ R implies that (a, c) ∈ R
Answer:
Given:
The set of rational numbers Q.
The relation R from Q to Q defined by R = $\{(a, b) : a, b \in Q \text{ and } a – b \in Z\}$.
To Show:
(i) $(a, a) \in R$ for all $a \in Q$.
(ii) If $(a, b) \in R$, then $(b, a) \in R$.
(iii) If $(a, b) \in R$ and $(b, c) \in R$, then $(a, c) \in R$.
Proof:
The relation R is defined by the condition that the difference between the first and second components of an ordered pair is an integer.
(i) Show that (a, a) ∈ R for all a ∈ Q.
Let $a$ be any element in Q ($a \in Q$).
To show that $(a, a) \in R$, we need to check if the difference between the components, $a – a$, is an integer.
$a - a = 0$.
Since $0$ is an integer ($0 \in Z$), the condition for $(a, a)$ to be in R is satisfied.
Therefore, $(a, a) \in R$ for all $a \in Q$. This shows that the relation R is reflexive.
(ii) Show that if (a, b) ∈ R, then (b, a) ∈ R.
Assume that $(a, b) \in R$.
By the definition of R, this means that $a \in Q$, $b \in Q$, and $a - b \in Z$.
Let $a - b = k$, where $k$ is some integer ($k \in Z$).
To show that $(b, a) \in R$, we need to check if $b \in Q$, $a \in Q$, and $b - a \in Z$.
We already know that $a \in Q$ and $b \in Q$ from the assumption.
Consider the difference $b - a$. We can relate it to $a - b$:
$b - a = -(a - b)$.
Since $a - b = k$, we have $b - a = -k$.
Since $k$ is an integer ($k \in Z$), its negative, $-k$, is also an integer ($-k \in Z$).
Thus, $b - a$ is an integer.
The condition for $(b, a)$ to be in R is satisfied.
Therefore, if $(a, b) \in R$, then $(b, a) \in R$. This shows that the relation R is symmetric.
(iii) Show that if (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R.
Assume that $(a, b) \in R$ and $(b, c) \in R$.
From $(a, b) \in R$, we know that $a \in Q$, $b \in Q$, and $a - b = k_1$ for some integer $k_1 \in Z$.
From $(b, c) \in R$, we know that $b \in Q$, $c \in Q$, and $b - c = k_2$ for some integer $k_2 \in Z$.
To show that $(a, c) \in R$, we need to check if $a \in Q$, $c \in Q$, and $a - c \in Z$.
We already know that $a \in Q$ and $c \in Q$ from the assumptions (since $a, b \in Q$ and $b, c \in Q$).
Consider the difference $a - c$. We can write this difference as the sum of the differences we know are integers:
$a - c = (a - b) + (b - c)$.
Substitute the values $k_1$ and $k_2$:
$a - c = k_1 + k_2$.
Since $k_1$ is an integer ($k_1 \in Z$) and $k_2$ is an integer ($k_2 \in Z$), their sum $k_1 + k_2$ is also an integer. Let $k_3 = k_1 + k_2$. Then $k_3 \in Z$.
Thus, $a - c$ is an integer.
The condition for $(a, c)$ to be in R is satisfied.
Therefore, if $(a, b) \in R$ and $(b, c) \in R$, then $(a, c) \in R$. This shows that the relation R is transitive.
Since the relation R is reflexive, symmetric, and transitive, it is an equivalence relation on Q.
Example 20: Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a linear function from Z into Z. Find f(x).
Answer:
Given:
The function $f$ is a linear function from Z to Z.
The function is given as a set of ordered pairs: $f = \{(1, 1), (2, 3), (0, –1), (–1, –3)\}$.
To Find:
The rule for the function, $f(x)$.
Solution:
Since $f$ is a linear function from Z to Z, it can be represented in the form $f(x) = mx + c$, where $m$ and $c$ are constants to be determined.
We are given several ordered pairs $(x, f(x))$ that belong to this function. We can use these points to find the values of $m$ and $c$.
Using the point $(0, -1)$: when $x = 0$, $f(x) = -1$. Substitute these values into the linear function form:
$f(0) = m(0) + c$
$-1 = 0 + c$
$c = -1$
So, the function is of the form $f(x) = mx - 1$.
Now, using another point from the set, say $(1, 1)$: when $x = 1$, $f(x) = 1$. Substitute these values into the partial function form $f(x) = mx - 1$:
$f(1) = m(1) - 1$
$1 = m - 1$
Add 1 to both sides:
$1 + 1 = m$
$m = 2$
Substitute the values of $m=2$ and $c=-1$ back into the linear function form $f(x) = mx + c$:
$f(x) = 2x + (-1)$
$f(x) = 2x - 1$
We can verify this rule with the other given points:
For $(2, 3)$: $f(2) = 2(2) - 1 = 4 - 1 = 3$. This matches the point $(2, 3)$.
For $(-1, -3)$: $f(-1) = 2(-1) - 1 = -2 - 1 = -3$. This matches the point $(-1, -3)$.
All given points satisfy the rule $f(x) = 2x - 1$.
Therefore, the function rule is f(x) = 2x - 1.
Example 21: Find the domain of the function f(x) = $\frac{x^{2} \;+\; 3x \;+\;5}{x^{2} \;-\; 5x \;+\;4}$
Answer:
Given:
The function $f(x) = \frac{x^2 + 3x + 5}{x^2 - 5x + 4}$.
To Find:
The domain of the function $f(x)$.
Solution:
The function $f(x)$ is a rational function, defined as the ratio of two polynomials. A rational function is defined for all real numbers where the denominator is not equal to zero.
To find the domain, we need to identify the values of $x$ for which the denominator is zero and exclude them from the set of real numbers R.
Set the denominator equal to zero:
$x^2 - 5x + 4 = 0$
This is a quadratic equation. We can solve it by factoring. We look for two numbers that multiply to 4 and add up to -5. These numbers are -1 and -4.
Factor the quadratic expression:
$(x - 1)(x - 4) = 0$
For the product of two factors to be zero, at least one of the factors must be zero.
Case 1: $x - 1 = 0$
$x = 1$
Case 2: $x - 4 = 0$
$x = 4$
So, the denominator is zero when $x = 1$ or $x = 4$. These are the values that are not in the domain of the function.
The function $f(x)$ is defined for all real numbers except 1 and 4.
Therefore, the domain of the function $f(x)$ is the set of all real numbers R minus the set $\{1, 4\}$.
Domain of $f = R – \{1, 4\}$.
Example 22: The function f is defined by
$f(x) = \begin{cases} 1 - x &,& x < 0 \\ 1 & ,& x = 0\\ x + 1 &,&x >0 \end{cases}$
Draw the graph of f (x).
Answer:
Given:
The piecewise function $f(x)$ is defined as:
$f(x) = \begin{cases} 1 - x & , & x < 0 \\ 1 & , & x = 0 \\ x + 1 & , & x > 0 \end{cases}$
To Draw:
The graph of the function $f(x)$.
Solution:
The function is defined by different rules for different intervals of the domain (all real numbers). We need to graph each part separately over its specified interval.
Case 1: $x < 0$
The function is $f(x) = 1 - x$. This is a linear function. The graph will be a straight line. We can find a few points for $x < 0$:
- If $x = -1$, $f(-1) = 1 - (-1) = 1 + 1 = 2$. Point: $(-1, 2)$.
- If $x = -2$, $f(-2) = 1 - (-2) = 1 + 2 = 3$. Point: $(-2, 3)$.
- Consider the point as $x$ approaches 0 from the left. As $x \to 0^-$, $f(x) = 1 - x \to 1 - 0 = 1$. The line segment approaches the point $(0, 1)$, but the point itself is not included in this part of the graph (represented by an open circle visually, although the point is covered by the $x=0$ case).
Case 2: $x = 0$
The function is $f(x) = 1$. This defines a single point on the graph.
If $x = 0$, $f(0) = 1$. Point: $(0, 1)$. This point is explicitly included in the graph (represented by a closed circle).
Case 3: $x > 0$
The function is $f(x) = x + 1$. This is also a linear function. The graph will be a straight line. We can find a few points for $x > 0$:
- If $x = 1$, $f(1) = 1 + 1 = 2$. Point: $(1, 2)$.
- If $x = 2$, $f(2) = 2 + 1 = 3$. Point: $(2, 3)$.
- Consider the point as $x$ approaches 0 from the right. As $x \to 0^+$, $f(x) = x + 1 \to 0 + 1 = 1$. The line segment approaches the point $(0, 1)$, but the point itself is not included in this part of the graph.
To sketch the graph:
1. Draw the horizontal x-axis and the vertical y-axis on a coordinate plane.
2. For the region $x < 0$, plot points like $(-1, 2)$ and $(-2, 3)$. Draw a straight line through these points. Since $x$ is strictly less than 0, this line segment extends infinitely to the left and approaches the point $(0, 1)$ but does not include it in this part of the definition.
3. For the point $x = 0$, plot the point $(0, 1)$ with a solid dot to show it is included in the graph.
4. For the region $x > 0$, plot points like $(1, 2)$ and $(2, 3)$. Draw a straight line through these points. Since $x$ is strictly greater than 0, this line segment extends infinitely to the right and starts visually from the point $(0, 1)$ but does not include it based on this part of the definition.
Combining these parts, the graph consists of two rays originating from (or ending at) the point (0, 1). The ray for $x < 0$ goes up and to the left (slope -1), and the ray for $x > 0$ goes up and to the right (slope 1). The point (0, 1) is included in the graph.
Miscellaneous Exercise on Chapter 2
Question 1. The relation f is defined by $f(x) = \begin{cases} x^2 &,& 0 \leq x \leq 3 \\ 3x &,& 3 \leq x \leq 10 \end{cases}$
The relation g is defined by $g(x) = \begin{cases} x^2 &,& 0 \leq x \leq 2 \\ 3x &,& 2 \leq x \leq 10 \end{cases}$
Show that f is a function and g is not a function.
Answer:
Given:
Relation f defined by $f(x) = \begin{cases} x^2 & , & 0 \leq x \leq 3 \\ 3x & , & 3 \leq x \leq 10 \end{cases}$
Relation g defined by $g(x) = \begin{cases} x^2 & , & 0 \leq x \leq 2 \\ 3x & , & 2 \leq x \leq 10 \end{cases}$
To Show:
f is a function.
g is not a function.
Solution:
A relation $R$ from a set A to a set B is a function if for every element $x$ in the domain of $R$, there is one and only one element $y$ in the codomain such that $(x, y) \in R$. In the context of the given relations defined by rules, this means that for each value of $x$ in the domain, the definition must yield a single unique value of $f(x)$ or $g(x)$.
This is particularly important to check at the boundary points where the definition of the relation changes.
Analysis of relation f:
The definition of $f(x)$ changes at $x=3$. The domain of $f$ is $[0, 10]$.
For $0 \leq x < 3$, $f(x) = x^2$. This rule gives a unique output for each input in this interval.
For $3 < x \leq 10$, $f(x) = 3x$. This rule also gives a unique output for each input in this interval.
Now, let's check the value at the boundary point $x=3$. The point $x=3$ is included in both intervals of the definition ($0 \leq x \leq 3$ and $3 \leq x \leq 10$).
Using the first rule ($f(x) = x^2$) for $x=3$:
$f(3) = (3)^2 = 9$
Using the second rule ($f(x) = 3x$) for $x=3$:
$f(3) = 3(3) = 9$
Since both rules give the same output value (9) for the input $x=3$, there is no ambiguity at the boundary point. For every value of $x$ in the domain $[0, 10]$, there is exactly one corresponding value of $f(x)$.
Therefore, f is a function.
Analysis of relation g:
The definition of $g(x)$ changes at $x=2$. The domain of $g$ is $[0, 10]$.
For $0 \leq x < 2$, $g(x) = x^2$. This rule gives a unique output for each input in this interval.
For $2 < x \leq 10$, $g(x) = 3x$. This rule also gives a unique output for each input in this interval.
Now, let's check the value at the boundary point $x=2$. The point $x=2$ is included in both intervals of the definition ($0 \leq x \leq 2$ and $2 \leq x \leq 10$).
Using the first rule ($g(x) = x^2$) for $x=2$:
$g(2) = (2)^2 = 4$
Using the second rule ($g(x) = 3x$) for $x=2$:
$g(2) = 3(2) = 6$
Since the two rules give different output values (4 and 6) for the same input $x=2$, the relation $g$ associates the element 2 with two different images (4 and 6). This violates the definition of a function, which requires each domain element to have exactly one image.
Therefore, g is not a function.
Question 2. If f(x) = x2 . find $\frac{f(1.1) \;-\; f(1)}{(1.1 \;-\; 1)}$ .
Answer:
Given:
The function $f(x) = x^2$.
The expression to evaluate is $\frac{f(1.1) - f(1)}{1.1 - 1}$.
To Find:
The value of the given expression.
Solution:
The function is $f(x) = x^2$. We need to find the values of $f(1.1)$ and $f(1)$ by substituting the respective values for $x$ in the function rule.
Calculate $f(1.1)$:
$f(1.1) = (1.1)^2$
$1.1 \times 1.1 = 1.21$.
$f(1.1) = 1.21$
Calculate $f(1)$:
$f(1) = (1)^2$
$f(1) = 1$
Now, calculate the denominator of the expression:
$1.1 - 1 = 0.1$
Substitute the calculated values into the given expression:
$\frac{f(1.1) - f(1)}{1.1 - 1} = \frac{1.21 - 1}{0.1}$
Calculate the difference in the numerator:
$1.21 - 1 = 0.21$
Now, perform the division:
$\frac{0.21}{0.1}$
To divide by a decimal, we can multiply the numerator and denominator by a power of 10 to make the denominator an integer. Multiply by 10:
$\frac{0.21 \times 10}{0.1 \times 10} = \frac{2.1}{1}$
$\frac{2.1}{1} = 2.1$
Therefore, the value of the expression is 2.1.
Question 3. Find the domain of the function f(x) = $\frac{x^2 \;+\; 2x \;+\; 1}{x^2 \;-\; 8x \;+\; 12}$ .
Answer:
Given:
The function $f(x) = \frac{x^2 + 2x + 1}{x^2 - 8x + 12}$.
To Find:
The domain of the function $f(x)$.
Solution:
The function $f(x)$ is a rational function. For a rational function to be defined in the set of real numbers, the denominator must not be equal to zero.
To find the domain, we need to find the values of $x$ for which the denominator is zero and exclude these values from the set of all real numbers R.
Set the denominator equal to zero:
$x^2 - 8x + 12 = 0$
This is a quadratic equation. We can solve it by factoring. We need to find two numbers that multiply to 12 and add up to -8. These numbers are -2 and -6.
Factor the quadratic expression:
$(x - 2)(x - 6) = 0$
For the product of two factors to be zero, at least one of the factors must be zero.
Case 1: $x - 2 = 0$
$x = 2$
Case 2: $x - 6 = 0$
$x = 6$
So, the denominator is zero when $x = 2$ or $x = 6$. These are the values that must be excluded from the domain of the function.
The function $f(x)$ is defined for all real numbers except 2 and 6.
Therefore, the domain of the function $f(x)$ is the set of all real numbers R minus the set $\{2, 6\}$.
Domain of $f = R – \{2, 6\}$.
Question 4. Find the domain and the range of the real function f defined by f(x) = $\sqrt{(x - 1)}$ .
Answer:
Given:
The real function $f(x) = \sqrt{x - 1}$.
To Find:
The domain of $f(x)$.
The range of $f(x)$.
Solution:
Domain of f(x):
For the function $f(x) = \sqrt{x - 1}$ to be defined as a real number, the expression under the square root must be non-negative (greater than or equal to zero).
So, we must have $x - 1 \ge 0$.
Add 1 to both sides of the inequality:
$x - 1 + 1 \ge 0 + 1$
$x \ge 1$
The domain of the function is the set of all real numbers $x$ such that $x$ is greater than or equal to 1.
Domain of $f = [1, \infty)$.
Range of f(x):
The range of the function is the set of all possible output values $f(x) = \sqrt{x - 1}$ for $x$ in the domain $[1, \infty)$.
Since the square root symbol $\sqrt{\phantom{a}}$ denotes the non-negative square root, the value of $f(x)$ will always be non-negative.
So, $f(x) \ge 0$.
Let's consider the values of $f(x)$ as $x$ varies in the domain $[1, \infty)$.
When $x = 1$, $f(1) = \sqrt{1 - 1} = \sqrt{0} = 0$. This is the minimum value of $f(x)$.
As $x$ increases from 1 towards $\infty$, the value of $x - 1$ increases from 0 towards $\infty$. Consequently, the value of $\sqrt{x - 1}$ increases from $\sqrt{0}=0$ towards $\sqrt{\infty}=\infty$.
The values of $f(x)$ can be any non-negative real number.
Thus, the range of the function is the set of all non-negative real numbers.
Range of $f = [0, \infty)$.
Question 5. Find the domain and the range of the real function f defined by f (x) = $|x – 1|$ .
Answer:
Given:
The real function $f(x) = |x - 1|$.
To Find:
The domain of $f(x)$.
The range of $f(x)$.
Solution:
Domain of f(x):
The domain of a real function is the set of all real numbers for which the function is defined.
The function $f(x) = |x - 1|$ involves taking the difference between $x$ and 1, and then taking the absolute value of the result. Both subtraction and the absolute value operation are defined for all real numbers $x$.
Therefore, the function $f(x) = |x - 1|$ is defined for all real numbers.
Domain of $f = R = (-\infty, \infty)$.
Range of f(x):
The range of a function is the set of all possible output values. The absolute value of any real number is always non-negative (greater than or equal to zero).
The expression inside the absolute value, $x - 1$, can take any real value as $x$ takes any real value (e.g., if $x = 5$, $x-1=4$; if $x=1$, $x-1=0$; if $x=-3$, $x-1=-4$).
The absolute value of $x - 1$, denoted by $|x - 1|$, is always non-negative.
$|x - 1| \ge 0$
So, the value of $f(x) = |x - 1|$ is always greater than or equal to 0.
The minimum value of $|x - 1|$ is 0, which occurs when $x - 1 = 0$, i.e., when $x = 1$. At $x=1$, $f(1) = |1 - 1| = |0| = 0$.
As $x$ moves away from 1 in either direction, the value of $|x - 1|$ increases and can take any positive real value. For example, to get an output of 5, we need $|x-1|=5$, which gives $x-1=5$ (so $x=6$) or $x-1=-5$ (so $x=-4$). Both $x=6$ and $x=-4$ are in the domain R, and $f(6)=|6-1|=5$ and $f(-4)=|-4-1|=|-5|=5$.
Thus, the values of $f(x)$ can be any non-negative real number.
Range of $f = [0, \infty)$.
The graph of $f(x) = |x - 1|$ is a 'V' shape with the vertex at the point where $|x-1|=0$, which is $(1, 0)$. The graph is symmetric about the vertical line $x=1$.
Question 6. Let $\left\{ \left( x, \frac{x^2}{1 \;+\; x^2} \right): x\in R \right\}$ be a function from R into R. Determine the range of f.
Answer:
Given:
The function is defined by $f(x) = \frac{x^2}{1 + x^2}$, and the domain is the set of all real numbers R, i.e., $x \in R$.
To Find:
The range of the function $f(x)$.
Solution:
The domain of the function is given as R, the set of all real numbers.
The range of the function is the set of all possible output values $y = f(x)$.
Consider the expression for $f(x)$: $f(x) = \frac{x^2}{1 + x^2}$.
For any real number $x$, $x^2 \ge 0$.
Also, $1 + x^2 \ge 1$ for all real $x$. Since $1 + x^2$ is always greater than or equal to 1, it is always positive and never zero.
Since the numerator $x^2 \ge 0$ and the denominator $1 + x^2 > 0$, the fraction $\frac{x^2}{1 + x^2}$ must be non-negative.
$f(x) \ge 0$
Now, let's find if there is an upper bound for $f(x)$. We can rewrite $f(x)$:
$f(x) = \frac{x^2}{1 + x^2}$
We know that $x^2 < 1 + x^2$ for all real $x$. Since $1 + x^2 > 0$, we can divide both sides of the inequality $x^2 < 1 + x^2$ by $1 + x^2$ without changing the direction of the inequality:
$\frac{x^2}{1 + x^2} < \frac{1 + x^2}{1 + x^2}$
$\frac{x^2}{1 + x^2} < 1$
So, $f(x) < 1$ for all real numbers $x$.
Combining the two inequalities, we have $0 \le f(x) < 1$.
When $x=0$, $f(0) = \frac{0^2}{1 + 0^2} = \frac{0}{1} = 0$. So, 0 is included in the range.
As $x$ becomes very large (positive or negative), $x^2$ becomes very large. The value of $f(x) = \frac{x^2}{1 + x^2}$ approaches 1, but never actually reaches 1.
For example, if $x=10$, $f(10) = \frac{100}{101} \approx 0.99$. If $x=100$, $f(100) = \frac{10000}{10001} \approx 0.9999$.
The function can take any value between 0 (inclusive) and 1 (exclusive).
Therefore, the range of the function $f(x)$ is the interval $[0, 1)$.
Range of $f = [0, 1)$.
Question 7. Let f, g : R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and $\frac{f}{g}$ .
Answer:
Given:
Two real functions $f: R \to R$ defined by $f(x) = x + 1$.
Two real functions $g: R \to R$ defined by $g(x) = 2x – 3$.
The domain of both $f$ and $g$ is R (the set of all real numbers).
To Find:
The sum function $(f + g)(x)$.
The difference function $(f – g)(x)$.
The quotient function $\left( \frac{f}{g} \right)(x)$.
Solution:
The operations on real functions are defined as follows:
1. Sum of functions (f + g)(x):
$(f + g)(x) = f(x) + g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(f + g)(x) = (x + 1) + (2x – 3)$
Combine like terms:
$(f + g)(x) = x + 2x + 1 - 3$
$(f + g)(x) = 3x - 2$
The domain of $(f + g)(x)$ is the intersection of the domains of $f$ and $g$, which is $R \cap R = R$.
2. Difference of functions (f – g)(x):
$(f – g)(x) = f(x) – g(x)$
Substitute the given expressions for $f(x)$ and $g(x)$:
$(f – g)(x) = (x + 1) - (2x – 3)$
Distribute the negative sign:
$(f – g)(x) = x + 1 - 2x + 3$
Combine like terms:
$(f – g)(x) = x - 2x + 1 + 3$
$(f – g)(x) = -x + 4$
The domain of $(f – g)(x)$ is the intersection of the domains of $f$ and $g$, which is $R \cap R = R$.
3. Quotient of functions $\left( \frac{f}{g} \right)(x)$:
$\left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)}$, provided $g(x) \neq 0$.
Substitute the given expressions for $f(x)$ and $g(x)$:
$\left( \frac{f}{g} \right)(x) = \frac{x + 1}{2x – 3}$
The domain of $\left( \frac{f}{g} \right)(x)$ is the intersection of the domains of $f$ and $g$, excluding the values of $x$ where $g(x) = 0$.
We need to find the values of $x$ for which $g(x) = 0$:
$2x – 3 = 0$
$2x = 3$
$x = \frac{3}{2}$
So, the domain of $\left( \frac{f}{g} \right)(x)$ is all real numbers except $\frac{3}{2}$.
Domain of $\left( \frac{f}{g} \right) = R – \{\frac{3}{2}\}$.
Summary of results:
$(f + g)(x) = 3x - 2$
$(f – g)(x) = -x + 4$
$\left( \frac{f}{g} \right)(x) = \frac{x + 1}{2x – 3}$, for $x \neq \frac{3}{2}$.
Question 8. Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Answer:
Given:
The function $f: Z \to Z$ is defined by $f(x) = ax + b$, where $a$ and $b$ are integers.
The function contains the ordered pairs: $(1, 1), (2, 3), (0, –1), (–1, –3)$.
To Find:
The values of the integers $a$ and $b$.
Solution:
Since the given ordered pairs are elements of the function $f$, they must satisfy the function rule $f(x) = ax + b$. We can substitute the $(x, f(x))$ values from these pairs into the equation to form a system of linear equations in terms of $a$ and $b$.
Using the ordered pair $(1, 1)$ where $x=1$ and $f(x)=1$:
$f(1) = a(1) + b$
$1 = a + b$
... (i)
Using the ordered pair $(0, -1)$ where $x=0$ and $f(x)=-1$:
$f(0) = a(0) + b$
$-1 = 0 + b$
$b = -1$
... (ii)
Now that we have the value of $b$, we can substitute it into equation (i) to find the value of $a$.
Substitute $b = -1$ into equation (i):
$1 = a + (-1)$
$1 = a - 1$
Add 1 to both sides of the equation:
$1 + 1 = a$
$a = 2$
... (iii)
We have found the values $a=2$ and $b=-1$. Both are integers, as required.
We can verify these values using the remaining ordered pairs:
Using the pair $(2, 3)$: $f(x) = 2x - 1$. $f(2) = 2(2) - 1 = 4 - 1 = 3$. This matches the given point.
Using the pair $(-1, -3)$: $f(x) = 2x - 1$. $f(-1) = 2(-1) - 1 = -2 - 1 = -3$. This matches the given point.
All given points are consistent with the function $f(x) = 2x - 1$, with $a=2$ and $b=-1$.
Therefore, the values are $a = 2$ and $b = -1$.
Question 9. Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
Answer:
Given:
The set of natural numbers N = $\{1, 2, 3, ...\}$.
The relation R from N to N defined by R = $\{(a, b) : a, b \in N \text{ and } a = b^2\}$.
To Verify and Justify:
(i) Is $(a, a) \in R$ for all $a \in N$?
(ii) If $(a, b) \in R$, does it imply $(b, a) \in R$?
(iii) If $(a, b) \in R$ and $(b, c) \in R$, does it imply $(a, c) \in R$?
Solution:
The relation R consists of ordered pairs $(a, b)$ of natural numbers such that the first component $a$ is the square of the second component $b$.
Let's list a few elements of R:
- If $b=1$, $a=1^2=1$. $(1, 1) \in R$.
- If $b=2$, $a=2^2=4$. $(4, 2) \in R$.
- If $b=3$, $a=3^2=9$. $(9, 3) \in R$.
- If $b=4$, $a=4^2=16$. $(16, 4) \in R$.
R = $\{(1, 1), (4, 2), (9, 3), (16, 4), \dots\}$. Note that $a$ must be a perfect square and $b$ its square root, where both are natural numbers.
(i) Is (a, a) ∈ R, for all a ∈ N?
For $(a, a)$ to be in R, we must have $a \in N$, and the first component must be the square of the second component, i.e., $a = a^2$.
We need to check if $a = a^2$ is true for all natural numbers $a \in \{1, 2, 3, ...\}$.
If $a = 1$, $1 = 1^2 = 1$. This is true. So $(1, 1) \in R$.
If $a = 2$, $2 = 2^2 = 4$. This is false. So $(2, 2) \notin R$.
If $a = 3$, $3 = 3^2 = 9$. This is false. So $(3, 3) \notin R$.
The condition $a = a^2$ is only true for $a=1$ in the set of natural numbers.
Since $(a, a) \notin R$ for all $a \in N$ (specifically not for $a=2, 3, 4, \dots$), the statement is False.
Justification: The statement is false because, for example, for $a=2 \in N$, $(2, 2) \notin R$ since $2 \neq 2^2$.
(ii) If (a, b) ∈ R, does it imply (b, a) ∈ R?
Assume that $(a, b) \in R$. By the definition of R, this means $a \in N$, $b \in N$, and $a = b^2$.
For $(b, a)$ to be in R, we must have $b \in N$, $a \in N$, and $b = a^2$.
We are given $a = b^2$. We need to check if $b = a^2$ necessarily follows from $a = b^2$ for $a, b \in N$.
Consider the element $(4, 2) \in R$, since $4 \in N$, $2 \in N$, and $4 = 2^2$.
Now check if $(2, 4) \in R$. For $(2, 4)$ to be in R, we must have $2 \in N$, $4 \in N$, and $2 = 4^2$.
$4^2 = 16$. Since $2 \neq 16$, $(2, 4) \notin R$.
We found a counterexample: $(4, 2) \in R$ but $(2, 4) \notin R$.
Therefore, the statement is False.
Justification: The statement is false because, for example, $(4, 2) \in R$ since $4 = 2^2$, but $(2, 4) \notin R$ since $2 \neq 4^2$.
(iii) If (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Assume that $(a, b) \in R$ and $(b, c) \in R$.
From $(a, b) \in R$, we know that $a \in N$, $b \in N$, and $a = b^2$.
From $(b, c) \in R$, we know that $b \in N$, $c \in N$, and $b = c^2$.
For $(a, c)$ to be in R, we must have $a \in N$, $c \in N$, and $a = c^2$.
We have $a = b^2$ and $b = c^2$. Substitute the expression for $b$ from the second equation into the first equation:
$a = (c^2)^2$
$a = c^4$
For $(a, c)$ to be in R, we need $a = c^2$. However, we found that if $(a, b) \in R$ and $(b, c) \in R$, then $a = c^4$.
The condition $a = c^4$ is generally not the same as $a = c^2$. For $a = c^4$ to be equal to $a = c^2$ (with $c \in N$), we would need $c^4 = c^2$, which implies $c^2(c^2 - 1) = 0$. Since $c \in N$, $c \ge 1$. $c^2 \ge 1$. So we must have $c^2 - 1 = 0$, which means $c^2 = 1$. Since $c \in N$, $c=1$. If $c=1$, then $b=c^2=1^2=1$ and $a=b^2=1^2=1$. In this specific case, $(1, 1) \in R$ and $(1, 1) \in R$, and $(1, 1) \in R$, so it holds. But this is not true for all cases.
Consider a case where $c > 1$. Let $c=2$.
If $c=2$, then $b=c^2 = 2^2 = 4$. Since $b=4 \in N$ and $c=2 \in N$, $(4, 2) \in R$.
Now, using $b=4$, find $a$ such that $(a, b) \in R$. $a = b^2 = 4^2 = 16$. Since $a=16 \in N$ and $b=4 \in N$, $(16, 4) \in R$.
So, we have $(16, 4) \in R$ and $(4, 2) \in R$. According to the statement, this should imply $(16, 2) \in R$.
For $(16, 2)$ to be in R, we need $16 \in N$, $2 \in N$, and $16 = 2^2$.
$2^2 = 4$. Since $16 \neq 4$, $(16, 2) \notin R$.
We found a counterexample: $(16, 4) \in R$ and $(4, 2) \in R$, but $(16, 2) \notin R$.
Therefore, the statement is False.
Justification: The statement is false because, for example, $(16, 4) \in R$ (since $16 = 4^2$) and $(4, 2) \in R$ (since $4 = 2^2$), but $(16, 2) \notin R$ (since $16 \neq 2^2$).
Question 10. Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
Are the following true?
(i) f is a relation from A to B
(ii) f is a function from A to B.
Justify your answer in each case.
Answer:
Given:
Set A = $\{1, 2, 3, 4\}$
Set B = $\{1, 5, 9, 11, 15, 16\}$
Set of ordered pairs $f = \{(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)\}$.
To Verify and Justify:
(i) Is $f$ a relation from A to B?
(ii) Is $f$ a function from A to B?
Solution:
(i) Is f is a relation from A to B?
A relation from set A to set B is defined as any subset of the Cartesian product A $\times$ B. The Cartesian product A $\times$ B is the set of all ordered pairs $(a, b)$ where $a \in A$ and $b \in B$.
To check if $f$ is a relation from A to B, we need to verify if every ordered pair $(x, y)$ in $f$ satisfies the condition that $x \in A$ and $y \in B$.
Let's examine each ordered pair in $f = \{(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)\}$:
- $(1, 5)$: Is $1 \in A$ and $5 \in B$? Yes, $1 \in \{1, 2, 3, 4\}$ and $5 \in \{1, 5, 9, 11, 15, 16\}$. This pair is in A $\times$ B.
- $(2, 9)$: Is $2 \in A$ and $9 \in B$? Yes, $2 \in \{1, 2, 3, 4\}$ and $9 \in \{1, 5, 9, 11, 15, 16\}$. This pair is in A $\times$ B.
- $(3, 1)$: Is $3 \in A$ and $1 \in B$? Yes, $3 \in \{1, 2, 3, 4\}$ and $1 \in \{1, 5, 9, 11, 15, 16\}$. This pair is in A $\times$ B.
- $(4, 5)$: Is $4 \in A$ and $5 \in B$? Yes, $4 \in \{1, 2, 3, 4\}$ and $5 \in \{1, 5, 9, 11, 15, 16\}$. This pair is in A $\times$ B.
- $(2, 11)$: Is $2 \in A$ and $11 \in B$? Yes, $2 \in \{1, 2, 3, 4\}$ and $11 \in \{1, 5, 9, 11, 15, 16\}$. This pair is in A $\times$ B.
Since every ordered pair in $f$ is an element of A $\times$ B, $f$ is a subset of A $\times$ B.
Therefore, the statement f is a relation from A to B is true.
(ii) Is f is a function from A to B?
A relation $f$ from a set A to a set B is a function from A to B if and only if:
1. The domain of $f$ is equal to set A.
2. Every element in A has one and only one image in B under the relation $f$. (Equivalently, no two distinct ordered pairs in $f$ have the same first element).
Let's check these conditions for the given set $f = \{(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)\}$.
First, determine the domain of the relation $f$. The domain is the set of all first components of the ordered pairs in $f$.
Domain of $f = \{1, 2, 3, 4, 2\}$. The set of unique first components is $\{1, 2, 3, 4\}$.
Comparing the domain of $f$ with set A: Domain of $f = \{1, 2, 3, 4\}$ and $A = \{1, 2, 3, 4\}$. The first condition is met: Domain of $f = A$.
Next, check if every element in the domain has a unique image. We look for repeated first elements in the ordered pairs:
- The first element 1 is paired with 5: (1, 5).
- The first element 2 is paired with 9: (2, 9).
- The first element 3 is paired with 1: (3, 1).
- The first element 4 is paired with 5: (4, 5).
- The first element 2 is also paired with 11: (2, 11).
We observe that the element 2 in the domain is associated with two different images in set B: 9 and 11. The ordered pairs (2, 9) and (2, 11) have the same first element (2) but different second elements (9 and 11).
This violates the second condition for a function (that each element in the domain must have a unique image).
Therefore, the statement f is a function from A to B is false.
Justification: The statement is false because the element 2 in set A has two distinct images under $f$, namely 9 and 11, as shown by the ordered pairs (2, 9) and (2, 11) in $f$. For a function, each element in the domain must have exactly one image.
Question 11. Let f be the subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify your answer.
Answer:
Given:
The set of integers Z.
The relation (subset of Z $\times$ Z) $f$ defined by $f = \{(ab, a + b) : a, b \in Z\}$.
The relation is defined such that the first component of an ordered pair is the product of two integers $a$ and $b$, and the second component is the sum of the same two integers $a$ and $b$, where $a, b$ can be any integers.
To Determine and Justify:
Is $f$ a function from Z to Z?
Solution:
For $f$ to be a function from Z to Z, two conditions must be met:
1. The domain of $f$ must be the entire set Z. (Every integer must be a possible value for the first component $ab$).
2. For every element in the domain (every possible value of $ab$), there must be one and only one corresponding element in the codomain Z (the value of $a+b$). (Equivalently, no two distinct ordered pairs in $f$ can have the same first element).
Let's test the second condition by looking for potential ordered pairs with the same first element but different second elements.
The first component is $ab$, and the second component is $a+b$. We need to find if there exist different pairs of integers $(a, b)$ that produce the same product $ab$ but different sums $a+b$.
Consider different pairs of integers $(a, b)$ and calculate their product $ab$ and sum $a+b$:
- Let $a=1, b=6$: Product $ab = 1 \times 6 = 6$. Sum $a+b = 1 + 6 = 7$. Ordered pair: $(6, 7)$.
- Let $a=2, b=3$: Product $ab = 2 \times 3 = 6$. Sum $a+b = 2 + 3 = 5$. Ordered pair: $(6, 5)$.
We have found two distinct ordered pairs in the relation $f$: $(6, 7)$ and $(6, 5)$. These two ordered pairs have the same first element (6) but different second elements (7 and 5).
According to the definition of a function, each element in the domain must be mapped to a unique element in the codomain. Since the first element 6 is mapped to both 7 and 5, the relation $f$ does not satisfy this condition.
Therefore, the relation $f$ is not a function.
Justification: The relation $f = \{(ab, a + b) : a, b \in Z\}$ is not a function from Z to Z because there exist elements in the domain (values of $ab$) that are associated with more than one element in the codomain (values of $a+b$). For example, when $a=1$ and $b=6$, we get the ordered pair $(1 \times 6, 1 + 6) = (6, 7) \in f$. However, when $a=2$ and $b=3$, we get the ordered pair $(2 \times 3, 2 + 3) = (6, 5) \in f$. Since the first component 6 is mapped to both 7 and 5, the relation is not a function.
Question 12. Let A = {9, 10, 11, 12, 13} and let f : A → N be defined by f (n) = the highest prime factor of n. Find the range of f.
Answer:
Given:
Set A = $\{9, 10, 11, 12, 13\}$.
Function $f: A \to N$ defined by $f(n) = \text{the highest prime factor of } n$.
To Find:
The range of the function $f$.
Solution:
The domain of the function is the set A = $\{9, 10, 11, 12, 13\}$. The range of the function is the set of all possible output values $f(n)$ for each $n$ in the domain A.
We need to find the highest prime factor for each element in set A:
- For $n = 9$: The prime factorization of 9 is $3 \times 3 = 3^2$. The only prime factor is 3. The highest prime factor of 9 is 3. So, $f(9) = 3$.
- For $n = 10$: The prime factorization of 10 is $2 \times 5$. The prime factors are 2 and 5. The highest prime factor of 10 is 5. So, $f(10) = 5$.
- For $n = 11$: The number 11 is a prime number. Its only prime factor is 11. The highest prime factor of 11 is 11. So, $f(11) = 11$.
- For $n = 12$: The prime factorization of 12 is $2 \times 2 \times 3 = 2^2 \times 3$. The prime factors are 2 and 3. The highest prime factor of 12 is 3. So, $f(12) = 3$.
- For $n = 13$: The number 13 is a prime number. Its only prime factor is 13. The highest prime factor of 13 is 13. So, $f(13) = 13$.
The output values of the function for the elements in the domain are $\{f(9), f(10), f(11), f(12), f(13)\} = \{3, 5, 11, 3, 13\}$.
The range of the function is the set of unique values in this collection.
Range of $f = \{3, 5, 11, 13\}$.
The range of the function f is {3, 5, 11, 13}.

